[mathjax]※ 文章中の長い数式はスクロールできます! ※ 著作権の都合上、問題全文は掲載できません。 問題はお手持ちのもので参照してください。
2019年大阪医科大学第2問
問1 $0.125 \ \mathrm{mol/L}$
問2 $2.31 \times 10^{-2} \ \mathrm{/s}$
問3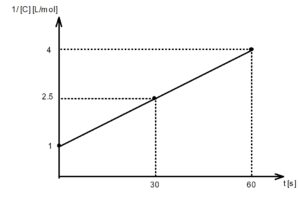
問4 $5.00 \times 10^{-2} \ \mathrm{L/mol・s}$
問5 $1.82 \times 10^{-1} \ \mathrm{mol/L}$
問1 表1において、$30$ 秒で濃度が半減していることが分かるので、$90$ 秒では、$$(\displaystyle \frac{ 1 }{ 2 })^3 = \displaystyle \frac{ 1 }{ 8 }$$ $$ ∴ 1.000\ \mathrm{mol/L} \times \displaystyle \frac{ 1 }{ 8 } = 0.125 (\mathrm{mol/L })$$
問2 問題文中より、反応速度 $v_1 = k_1 [\mathrm{A}]$ は、$$\log_e {\displaystyle \frac{ [\mathrm{A}]_t }{ [\mathrm{A}]_0}} = -k_1 t$$と表せるとある。(※証明は下の補足1にて。)
表1の$30$ 秒のときの値を用いると、$$\log_e {\displaystyle \frac{ 0.500 }{ 1.000 }} = -30k_1$$ $$-\log_e 2 = -30k_1$$ $$k_1 = \displaystyle \frac{ \log_e 2 }{ 30 } ≒ 2.31 \times 10^{-2}$$
単位については、求める単位を $\mathrm{X}$ とすると、$v_1 = k_1 [\mathrm{A}]$より、$$\mathrm{mol/L・s = X ・mol/L}$$ $$\mathrm{X = 1/s}$$
問3 グラフの縦軸が濃度 [C] の逆数であることに注意して点を打っていくと、直線になる。
問4 問題文中より、$v_2 = k_2 [\mathrm{C}]^2 $から、$$\displaystyle \frac{ 1 }{ [\mathrm{C}]_t } – \displaystyle \frac{ 1 }{ [\mathrm{C}]_0} = k_2 t $$ で表せるとある。 (※証明は下の補足にて。)
$$k_2 = \displaystyle \frac{ \displaystyle \frac{ 1 }{ [\mathrm{C}]_t }- \displaystyle \frac{ 1 }{ [\mathrm{C}]_0 } }{ t }$$ と変形できるので、 $k_2$ は問3のグラフの傾きである。$$k_2 = \displaystyle \frac{ 2.5 – 1 }{ 30 } = 0.0500$$
単位については、求める単位を $\mathrm{Y}$ とすると、$v_2 = k_2 [\mathrm{C}]^2$より、$$\mathrm{mol/L・s = Y ・(mol/L)^2}$$ $$\mathrm{Y = L/mol・s}$$
問5
$\displaystyle \frac{ 1 }{[\mathrm{C}]_{90} } – 1 = 0.05 \times 90 $ より、
$[\mathrm{C}]_{90} = \displaystyle \frac{ 1 }{ 5.5 } = 0.1818 … $



