- 受験化学で言われる「不飽和度」とは一体何なのか?
- 不飽和度の計算方法は分かるけれど、結局何に使うのか?
この記事では上記の疑問にできるだけ答えていきます。
高校化学全体の勉強法やおすすめの参考書はコチラから読めます!
構造決定の強い味方ー不飽和度とはー
「炭素数 $x$ に結合できる水素原子の最大数 $2x+2$」と
「今考えている分子中の実際の水素原子の数」の差を 2 で割ったものを
不飽和度(ここでは $U$ で表すことにする)といいます。
分子式 $\ce{C_{x}H_{y}O_{z}}$ における不飽和度 $U$ は、$$U=\displaystyle \frac{(2x+2)-y}{ 2 }$$ $$U=\displaystyle \frac{\small{(\mbox{$\ce{H}$原子の最大数})-(\mbox{実際の$\ce{H}$原子の数})}}{ 2 }$$で表される。
さらに、分子式 $\ce{C_{x}H_{y}O_{z}N_{w}}$ における不飽和度 $U$ は、$$U=\displaystyle \frac{(2x+2+w)-y}{ 2 }$$で表される。
不飽和度 $U$ が出たあとは次のことが分かります。
| $U=0$ | 単結合のみ、環状構造なし |
| $U=1$ | 二重結合 1 つ $\ce{C=C,\ C=O}$ 環状構造1つ |
| $U=2$ | $「U=1」 \times 2$ 三重結合1つ $\ce{C≡C}$ |
| $U=4$ | ベンゼン環 1つを含む可能性が高い (「$\ce{C=C \times 3 +}$ 環状構造」と考える。) |
なぜこのように考えられるかは後ほど記します。
不飽和度を実際に使ってみる
$\ce{C3H8}$
不飽和度 $U$ は、$$\displaystyle \frac{(2\times3+2)-8}{ 2 }=0$$
故に単結合がなく、環状構造もない構造式を考えれば良いことが分かります。
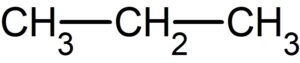
プロパンのみが該当します。
$\ce{C4H8}$ の異性体
不飽和度 $U$ は、$$\displaystyle \frac{(2\times4+2)-8}{ 2 }=1$$
故に二重結合を1つ持つか、環状構造を1つ持ちます。
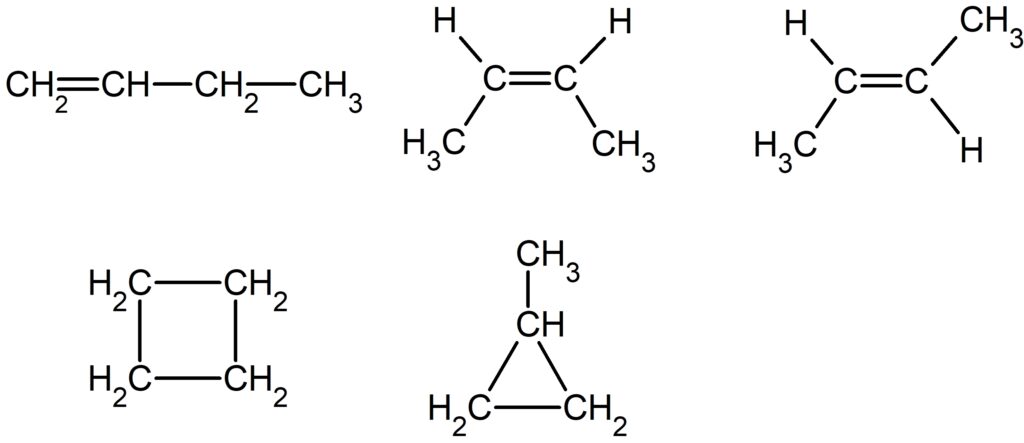
上段の左から順に
1 – ブテン、シス – 2 – ブテン、トランス – 2 – ブテン
下段の左から順に
シクロブタン、メチルシクロプロパンです。
$\ce{C7H8O}$の芳香族化合物の構造異性体
不飽和度 $U$ は、$$\displaystyle \frac{(2\times7+2)-8}{ 2 }=4$$
芳香族化合物とあるのでベンゼン環で $U=4$ を消費します。
あとは置換体の数で場合分けして考えれば良いです。
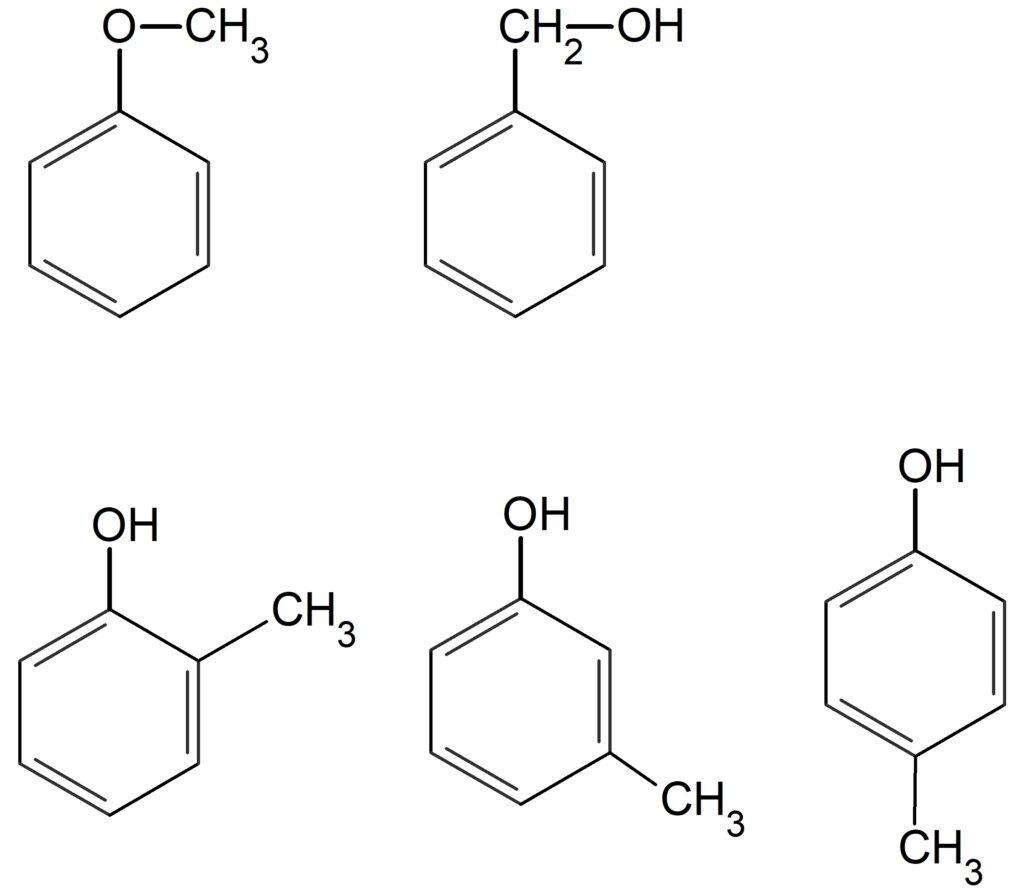
上段の左から順に、
メチルフェニルエーテル(メトキシベンゼン)、ベンジルアルコール
下段の左から順に、
o – クレゾール、m – クレゾール、p – クレゾールです。
不飽和度の式は、飽和のときからどれだけ水素が不足しているかを意味する
炭化水素における不飽和度の式の意味と導出
炭素と水素のみからなる化合物(炭化水素) $\ce{C_{x}H_{y} }$ について考えます。
もし環状ではなく単結合のみ(飽和鎖式炭化水素 / アルカン)であれば、
$\ce{C}$ 原子と結合する $\ce{H}$ 原子の最大数は $2x+2$ 個です。
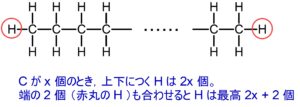
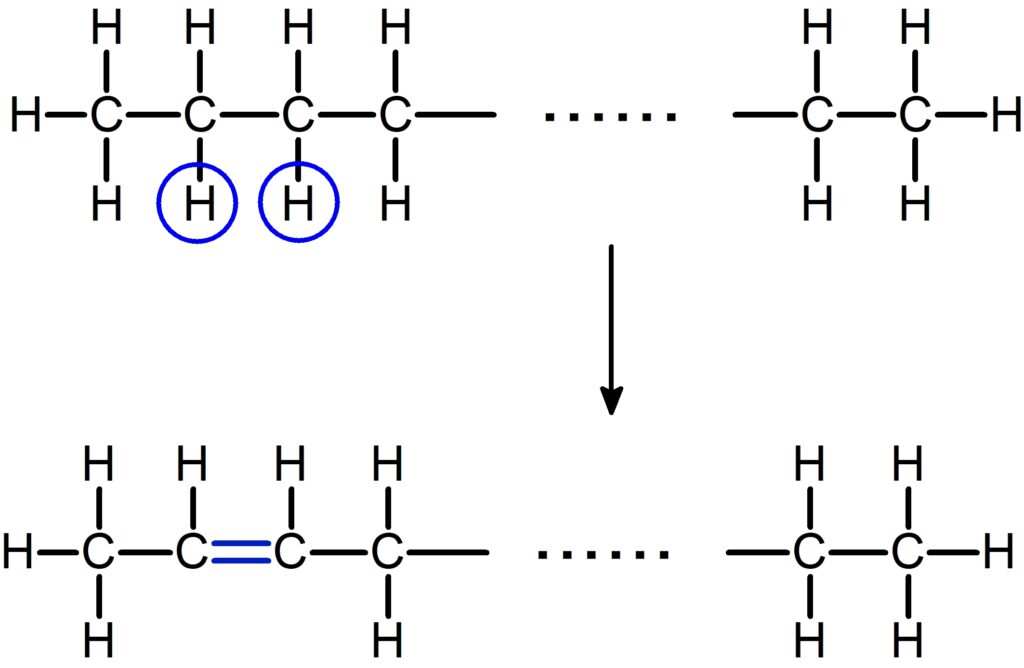
ここから炭素間二重結合を 1 つ付けるには、
下の図のように $\ce{H}$ を 2 つ取れば良いです。
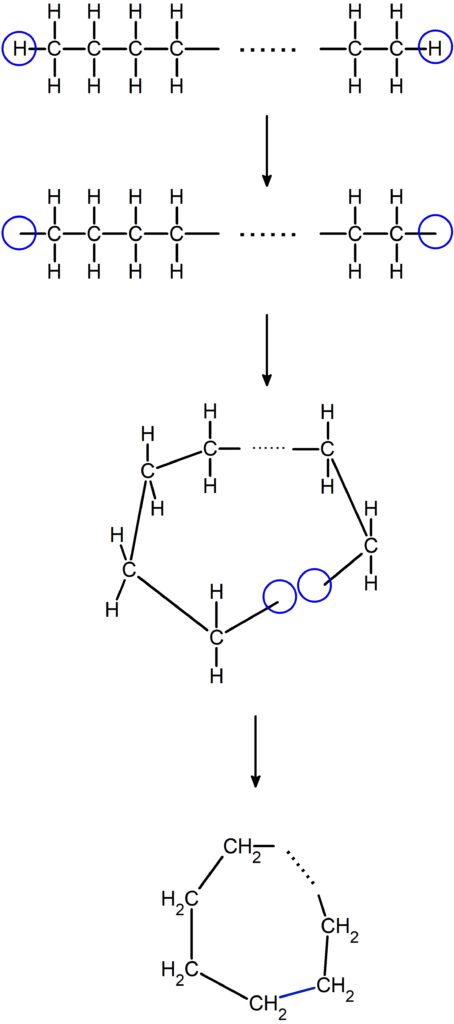
環状構造を 1 つ作るときは、端の $\ce{H}$ を 2 個とって繋げれば良いです。
以上のように、
二重結合を 1 つ付ける、または環状構造を 1 つ作ることは
$\ce{H}$ 原子を 2 つ取ることと同じです。(★)
さて、飽和炭化水素のときの $\ce{H}$ 原子の個数から
今考えている炭化水素の $\ce{H}$ 原子の個数を引けば、
いくつ $\ce{H}$ 原子がとれたかが分かります。
これは、飽和のときからどれだけ水素が不足しているかを意味しています。
例を挙げると、
例 $\ce{C5H10}$ はどのような炭化水素か。
炭素数 5 の飽和炭化水素(アルカン)であれば、分子式は $\ce{C5H12}$ である。
よって $12 – 10 = 2$ で $\ce{H}$ が $2$ 個取れたことが分かる。
この結果と(★)の結果をあわせて考えれば、
二重結合または環状構造の数が推測できます。
先の例でいくと、
$\ce{C5H10}$ は飽和炭化水素から $\ce{H}$ 原子が $2$ 個取れている= $2$ 個不足しているので、
二重結合が $1$ つ、または環状構造が $1$ つ存在することが分かる。
もう1つ例を挙げておこう。
$\ce{C7H12}$ を考える。
炭素数 7 の飽和炭化水素(アルカン)であれば、分子式は $\ce{C7H16}$ である。
よって $16 – 12 = 4$ で $\ce{H}$ が $4$ 個不足していることが分かる。
$\ce{H}$ 原子が $2$ 個不足していると
二重結合が $1$ つまたは環状構造が $1$ つあることが分かるので、
$\ce{C7H12}$ は
二重結合が $2$ つまたは環状構造が $2$ つ
または二重結合と環状構造を $1$ つずつ持つ化合物であることが分かる。
$\ce{H}$ 原子が $2$ 個不足していると
二重結合が $1$ つ、または環状構造が $1$ つできます。
数値に着目すると数字が $2$ で割られていることに気づくでしょう。
割った後の数字がそのまま二重結合の個数や環状構造の個数に直結しているため、
構造決定の問題を解くときに便利です。
これまでの話により、以下の公式が完成します。
分子式 $\ce{C_{x}H_{y} }$ における不飽和度 $U$ は、$$U=\displaystyle \frac{(2x+2)-y}{ 2 }$$で表される。
酸素原子をもつ有機化合物における不飽和度の式の意味と導出
アルコール $\ce{-OH}$ やエーテル $\ce{- O -}$ の場合は、
もとの炭化水素に酸素原子 $\ce{O}$ を挟み込むだけです。
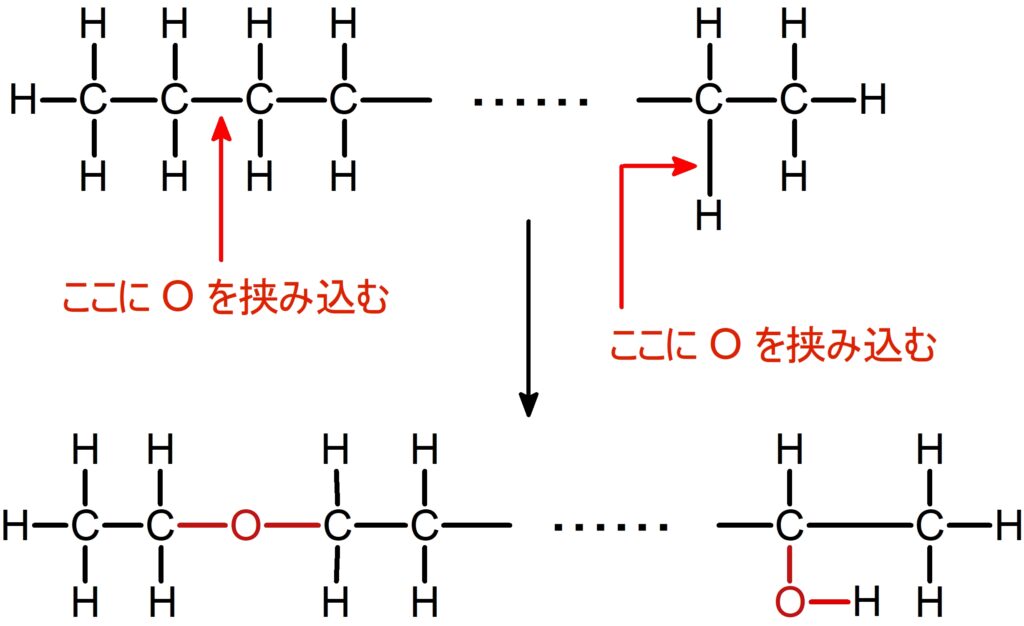
アルコールやエーテルの酸素原子は
水素原子の数に影響を与えません。
また、カルボニル $\ce{C=O}$ の酸素原子は下図のように考えると良いです。
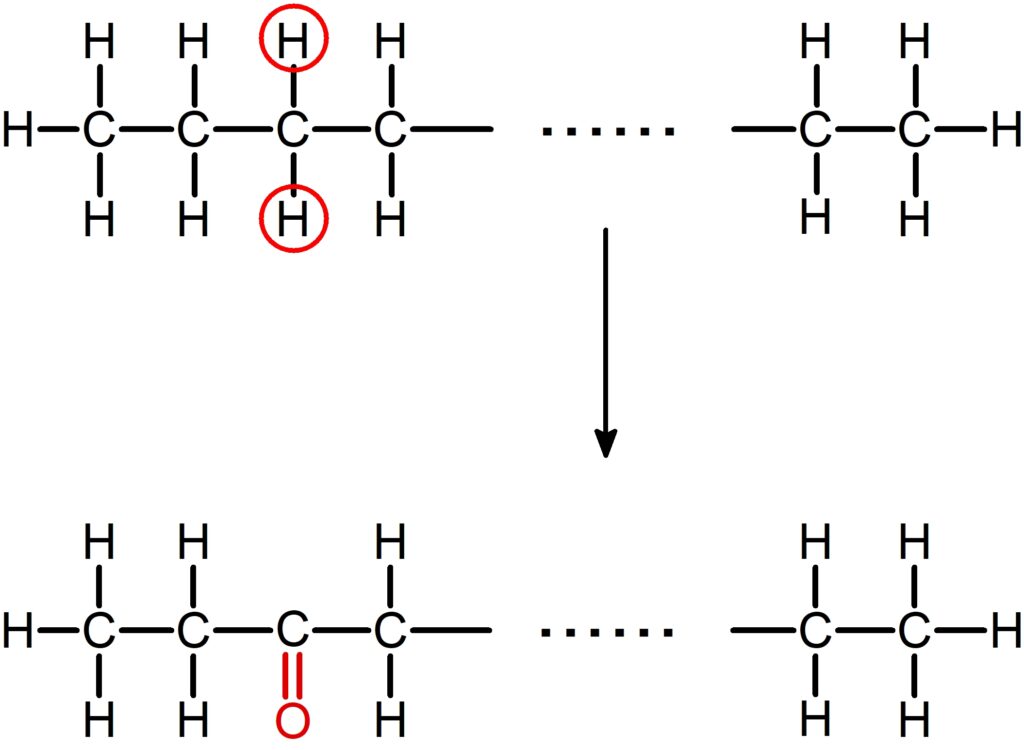
$\ce{H}$ 原子を $2$ つ取って、$\ce{O}$ 原子を付けるので、
炭化水素のときと同様に考えることができます。
すなわち、$\ce{H}$ が $2$ つ減っていてかつ $\ce{O}$ があれば、
$\ce{C=O}$ が存在する可能性があるということです。
以上の話を踏まえると、$\ce{O}$ 原子があっても
不飽和度の計算方法は変わらないことが分かります。
分子式 $\ce{C_{x}H_{y}O_{z} }$ における不飽和度 $U$ は、$$U=\displaystyle \frac{(2x+2)-y}{ 2 }$$で表される。
窒素原子をもつ有機化合物における不飽和度の式の意味と導出
$\ce{N}$ 原子の場合も $\ce{O}$ 原子の場合と同様で、
もとの炭化水素に挟み込むように考えれば良いです。
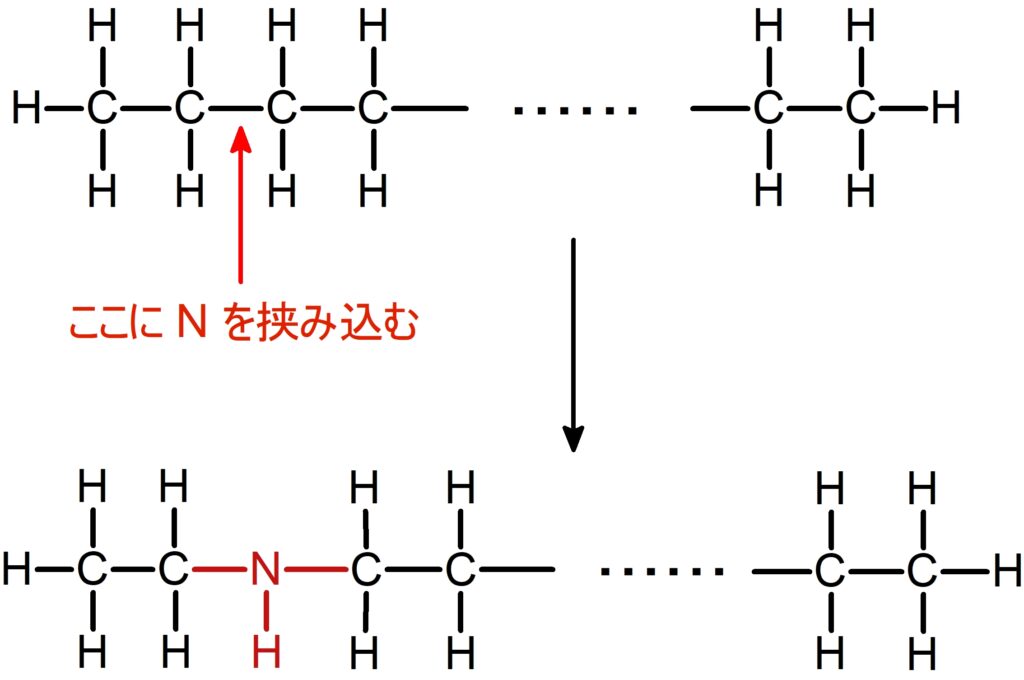
挟み込むと、付くことができる $\ce{H}$ 原子の数は
むしろ $1$ 増えます。
よって $\ce{N}$ 原子が $w$ 個あれば、$\ce{H}$ 原子の最大数も $w$ 個増えます。
このことから、$\ce{N}$ 原子を含んだ不飽和度の公式が得られます。
分子式 $\ce{C_{x}H_{y}O_{z}N_{w} }$ における不飽和度 $U$ は、$$U=\displaystyle \frac{(2x+2+w)-y}{ 2 }$$で表される。
今回は不飽和度を扱いました。
以下のページには構造異性体に特化して記事を書いているので、
こちらも参考にしてみてください。
【記事 執筆中】



