- 理論化学は大事だと聞くが、どのような単元があるのか知りたい。
- $\pu{mol}$ を使った計算問題が解けない。
- 各単元の何ができるようになれば良いのか分からない。
この記事では上の悩みを解決するため、$15$ 年間講師をしている著者が理論化学の単元の紹介と勉強法を解説していきます。
高校化学全体の勉強法やおすすめの参考書はコチラから読めます!
高校における理論化学の重要性
化学の4領域のうちの1つである理論化学。
大学入試の問題では出題割合の半数以上を占めています。
入試化学の中心と言っても良いでしょう。
理論化学といえば計算問題が多いという印象を持たれますが、
化学そのものの概念や考え方が詰まった領域でもあるので、無機化学や有機化学でも理論化学の知識を使います。
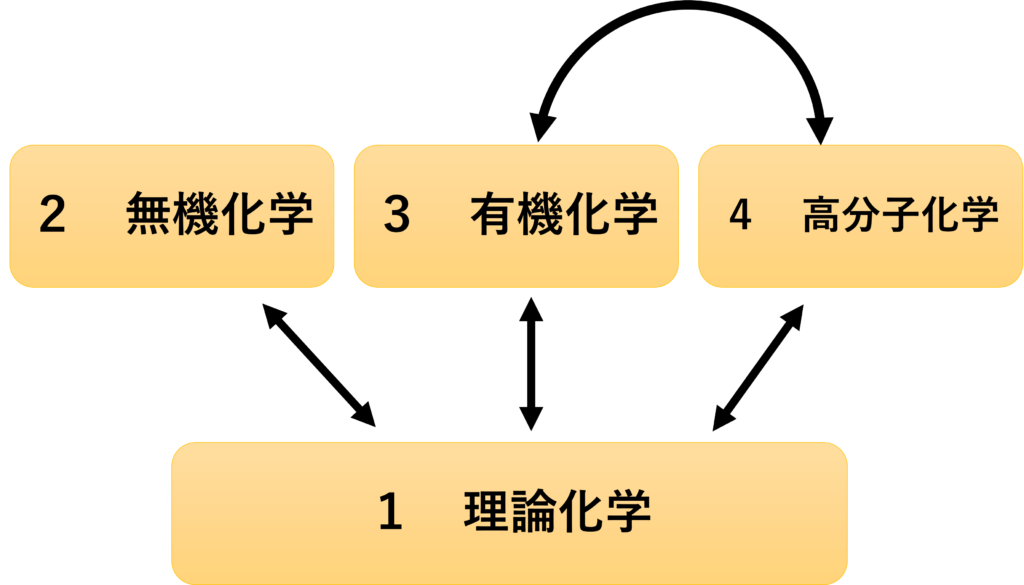
理論化学は、無機化学・有機化学・高分子化学のどの領域よりも優先して勉強しましょう。
理論化学の単元一覧と勉強法
高校化学の勉強法は、教科書を 1 節 ( 1 章)だけ精読した後にその節の範囲で問題集の問題を解き、解説を読み込む。
間違えた問題・分からなかった問題はチェックをつけておき、日を空けて自力で正解できるか確認をする。
極論をいえばこれを繰り返すだけです。
理論化学でも当てはまります。
( 冒頭に紹介した「高校化学全体の勉強法」の記事でも紹介しています。 )
以下では理論化学の単元と、
各単元で確実にできるようになっておきたいことのリストを紹介しています。
できるだけ教科書で出てくる順番になるようにしています。
この内容は外してはダメだ!というリストです。
リストの内容の問題が出たら反射的に解ける・説明できるようにしましょう。
物質の構成 | 化学基礎


- 物質はどのような粒子で構成されているのだろう?
- 粒子同士はどのような力や結合でまとまって存在するのだろう?
この2つを理解することが単元の目的です。
計算問題はほとんど出てきません。
中学理科の内容もわずかに被る箇所があるので
とっつきやすい単元です。
物質の成分と構成元素
- 物質を、純物質と混合物に分けられる。
(例:二酸化炭素は純物質、空気は混合物。) - 混合物の分離方法の意味と代表例が言える。
(例:原油は液体どうしの混合物を沸点の差で分けるので、分留をおこなう。) - 分離方法のうち特に頻出である蒸留について、実験器具の名前と操作方法の注意点が言える。
(例:枝付きフラスコに入れる液体は半分以下である。リービッヒ冷却器の水の流す向き、など。) - 同素体の定義と、$\ce{S, C, O, P}$の同素体の名称・性質が言える。
(例:$\ce{P}$ の同素体は黄リンと赤リンで、黄リンは自然発火するので水中に保存する。) - 元素 $\ce{Cl, C, H}$ の確認方法と、炎色反応による元素の確認方法が言える。
(例:ある物質を溶かした水溶液に硝酸銀水溶液を加えると白色沈澱が生じた。このとき、ある物質には$\ce{Cl}$ が含まれることが分かる。) - 固体・液体・気体間の状態変化の名称と、粒子の熱運動・粒子間の引力の大きさの違いを使って各状態変化の説明ができる。
(例:固体に熱を加えると粒子の熱運動が激しくなり、規則正しい配置が乱れて液体となる融解が起こる。)
元素の周期表、原子
- 質量数・原子番号の意味とその書き表し方が分かる。その表記から電子数・中性子数・陽子数が出せる。
(例: $\ce{ ^{13}_{6}C}$ の電子数は $6$, 中性子数は $7$, 陽子数は $6$ である。) - 同位体とは何か、水素や炭素を例に挙げて説明できる。同位体どうしの原子の構造の違いを理解する。
(例: $\ce{ ^{1}_{1}H}, \ce{ ^{2}_{1}H}, \ce{ ^{3}_{1}H}$ のように原子番号が同じで質量数の異なる原子どうしを互いに同位体という。) - 原子番号 $1 \sim 36$ の原子の周期表を覚える。原子番号 $1 \sim 20$ の原子の電子配置を書ける。
(例:$\ce{_{20}Ca}$ の電子配置は K($2$)L($8$)M($8$)N($2$) である。) - 周期表の同族に含まれる元素群の名称がいえる。
周期表上で金属元素と非金属元素・遷移元素と典型元素が区別でき、陽性・陰性の大きさの大小が比較できる。
(例:$17$ 族はハロゲンとよばれる。)
イオン・分子・金属と化学結合
- イオン化エネルギー・電子親和力の定義が言える。
- イオン半径の比較ができる。
(例:同族のイオン $\ce{Li+} < \ce{Na+}$ 、
同じ電子配置のイオン $\ce{Mg^2+} < \ce{Na+} < \ce{F-} < \ce{O^2-}$) - イオン結晶の性質と組成式が言える。
- 電子式が書ける。電子式を使って共有結合と配位結合が説明できる。
- 極性分子と無極性分子の違いを説明できる。分子の形が言える。
(例:メタン $\ce{CH4}$ は無極性分子で正四面体形。) - 金属結晶の性質を、自由電子と結びつけて説明できる。
- 物質を共有結合の結晶・分子結晶・イオン結晶・金属結晶のいずれかに分類でき、各結晶の性質や結晶内に含まれる力や結合が言える。
(例:ドライアイス $\ce{CO2}$ の結晶は分子結晶で、結晶内にはファンデルワールス力(分子間)・共有結合(分子内)が含まれる。)
物質の変化 | 化学基礎


こちらは計算問題が主になってきます。
物質量 ( モル、$\pu{mol}$ ) の計算は単なる比です。
また、濃度 (質量パーセント濃度 %、モル濃度 $\pu{mol/L}$、質量モル濃度 $\pu{mol/kg}$ )もやはり単なる比です。
定義をしっかり理解して覚えたうえで、 単位どうしの計算を意識すればスグに問題が解けるようになります。
物質量 ( モル ) と化学反応式
- 原子の相対質量と同位体の存在割合から原子量が計算できる。
(例:$\ce{^{12}C}$ と $\ce{^{13}C}$ の存在比を $98.9$ % と $1.1$ % とし、相対質量が質量数と等しいと近似すれば、炭素の原子量は $12 \times \f{98.9}{100} + 13\times \f{1.1}{100} = 12.011$ で $12.0$ と求まる。) - 原子量から分子量・式量を計算することができる。物質によって原子量・分子量・式量のうちどの言葉を使うのかが適切に選べる。
(例:$\ce{H}=1.0, \ce{O}=16, \ce{S}=32, \ce{Cu}=64$ を用いると、$\ce{CuSO4.5H2O}$ の式量は$250$ である。 ) - 物質量 [ $\pu{mol}$ ] と粒子数・質量 ・$0$℃, $\pu{1.013E5 Pa}$ ( 標準状態 ) の気体の体積の換算が自在にできる。
(例:$\ce{NH3}\ \pu{2 mol}$ は $\pu{1.2E24}$個、$\pu{34 g}$、標準状態で $\pu{44.8 L}$ である。) - 質量パーセント濃度やモル濃度を使った計算と、各濃度間の変換ができる。
(例:$98$ % の濃硫酸のモル濃度は密度 $\pu{1.80 g/cm^3}$ を用いると、溶液 $\pu{1.0 L}$ で考えて$$\pu{1.80 g/cm^3} \times \pu{1000 cm^3} \times \f{98}{100} \times \f{1}{\pu{98 g/mol}} \div \pu{1.0L} = \pu{18 mol/L}$$と計算できる。) - 化学変化を化学反応式で表せる。特に燃焼反応は問題文で生成物が与えられなくても書ける。
(例:メタンの燃焼反応は $\ce{CH4 + 2O2 -> CO2 + 2H2O}$ と書ける。) - 化学反応式の係数を用いて反応における計算問題が解ける。
(例:メタンを $\pu{1.0 mol}$ 、酸素を $\pu{5.0 mol}$ 容器に入れてメタンを完全燃焼させると、上の反応式の係数比を用いて、酸素が $\pu{3.0 mol}$ 余り、二酸化炭素が $\pu{1.0 mol}$ 生成する。)
酸と塩基・中和・pH
- アレニウスの定義、ブレンステッド・ローリーの定義、それぞれにおける酸・塩基の定義が言える。
- アレニウスの定義における強酸・弱酸・強塩基・弱塩基の物質の分類ができ、価数が言える。
(例: 硫酸 $\ce{H2SO4}$ は $2$ 価の強酸である。) - 電離度の概念を理解し、酸や塩基のモル濃度から pH が計算できる。
(例:$\pu{0.050 mol/L}$ の希硫酸の pH は、価数が $2$ 価、電離度が $1$ であることから、$0.050 \times 2 \times 1 = 0.10 = \pu{1.0E-1} $ より、 pH$=1$ と求まる。) - 塩の分類と、塩が水に溶けた水溶液の液性が言える。
なぜその液性になるのか塩の加水分解を用いて説明ができる。
(例:塩化アンモニウム $\ce{NH4Cl}$ は正塩で、$\ce{NH4^+ + H2O -> NH3 + H3O+}$ と反応するため、溶液は酸性である。) - 中和反応に関する計算問題ができる。
(例:$\pu{0.10 mol/L}$ の塩酸 $\pu{10 mL}$ を過不足なく中和するのに必要な $\pu
{0.20 mol/L}$ の水酸化カルシウムの体積は何 $\pu{mL}$ か。
求める体積を $x\ \pu{mL}$ とおくと
$\begin{align}
0.10 \times \f{10}{1000} \times 1 &= 0.20 \times \f{x}{1000} \times 2 \\
x &= 2.5
\end{align}$
$\pu{2.5 mL}$ と求まる。) - 中和滴定に用いる実験器具・指示薬がいえる。反応によってどの指示薬を使うのかが分かる。
特に「食酢中の酢酸のモル濃度の決定」の問題が解ける。
酸化・還元
- 酸化・還元の定義を $\ce{O, H, e-}$ のやりとりに注目して言える。
- 酸化数を算出することができ、化学反応式において酸化数の変化から酸化剤・還元剤が判別できる。
(例: $\ce{MnO2 + 4HCl -> MnCl2 + Cl2 + 2H2O}$ において、$\ce{Mn}$の酸化数が $+4 \rightarrow +2$ と減少しているので $\ce{MnO2}$ は酸化剤。$\ce{Cl}$ の酸化数が $-1 → 0$ と増加しているので還元剤。) - 半反応式が書けるようになり、酸化還元反応の化学反応式が書ける。
- 酸化還元反応の計算問題を、$\ce{e-}$ のやりとりに注目して解く方法と、化学反応式の係数比に注目して解く方法の両方ができるようになる。
- 金属のイオン化傾向を覚えて、反応性の違いを説明できる。
- 電池・電気分解の反応式と計算ができる。
- 金属の精錬を酸化還元反応の観点から説明できる。
物質の状態


物質の三態
- 状態変化における熱の出入りを説明できる。
(例:凝縮は構成粒子の熱運動の激しい気体から熱運動が穏やかな液体に変化するため、熱エネルギーは外部に放出される。) - 物質の融点・沸点を、化学結合や分子間力と結びつけて説明できる。
(例:$17$族元素の水素化合物は、$\ce{HCl, HBr, HI}$ の順に沸点が上がっていく。これは分子量が大きくなると、ファンデルワールス力が強くなるためである。しかし、$\ce{HF}$ は他のどの $3$ つよりも分子量が小さいにも関わらず沸点が高い。これは $\ce{HF}$ が分子間で水素結合を形成しているためである。) - 気体の圧力と分子の熱運動の関係が説明でき、$\pu{mmHg}$ と $\pu{Pa}$ と $\pu{atm}$ の単位の換算ができる。
- 気液平衡を理解し、蒸気圧曲線を使った問題を解くことができる。
- 沸騰を、大気圧と蒸気圧の関係から説明できる。
- 状態図を読み取ることができる。
気体の性質
- ボイルの法則・シャルルの法則の定義が言えて、これらやボイル・シャルルの法則を使った計算ができる。
- $PV = nRT$ をボイル・シャルルの法則から導けて、それを使った問題が解ける。
- 蒸気密度法による分子量測定の実験問題が解ける。
- 分圧の定義が言えて、モル分率を使って全圧と分圧の関係が言える。
- 水上置換法による分子量測定実験の問題が解ける。
- 混合気体で $\ce{H2O}$ があるとき、液体の存在が不明な場合の問題が解ける。
- 実在気体を理想気体とみなせる条件が説明できる。
溶液の性質
- 物質の溶解の仕方の違いを、溶質や溶媒の性質の違いから説明できる。
- 固体の溶解度や結晶の析出量の計算問題が解ける。溶解度曲線を用いた再結晶の説明と析出量の計算ができる。
- 気体の溶解度について、ヘンリーの法則を用いた問題が解ける。
- 希薄溶液の性質について、蒸気圧降下の話から、沸点上昇の話につなげて説明ができる。
- 浸透の原因と浸透圧の定義が説明できる。
- 沸点上昇度・凝固点降下度・浸透圧の計算問題が解ける。
- コロイドの種類が説明でき、コロイド溶液の性質が説明できる。
- 疎水コロイドと親水コロイドの違いや沈殿操作の違いが説明できる。
固体の構造
- 結晶と非晶質の違い、単位格子、配位数の概念が説明できる。
- 金属結晶のうち、体心立方格子・面心立方格子・六方最密構造の特徴が説明できる。
(例:体心立方格子の単位格子中の原子は $2$ 個で配位数は $8$ 、充填率は計算で $68$ % と出せる。
単位格子の一辺の長さを $a$ 、金属の原子半径を $r$ とすると、 $r = \f{\sqrt{3}}{4}a$ と書ける。) - イオン結晶のうち、 $\ce{CsCl}$ 型・$\ce{NaCl}$ 型・$\ce{ZnS}$ 型の特徴が説明できる。
(例: $\ce{CsCl}$ 型の配位数は $8$ で、単位格子中に $\ce{Cs+, Cl-}$ を $1$ 個ずつ含む。) - ヨウ素やドライアイスの結晶が昇華しやすい理由を説明できる。
- 氷が水に浮く理由と水の密度が $4$℃ で最大である理由を、結晶構造と結びつけて説明できる。
- ダイヤモンドと黒鉛の性質の違いを結晶構造から説明できて、それぞれの密度を算出できる。
物質の変化と平衡


熱化学・光化学
- 発熱反応と吸熱反応を、エネルギー図を用いて説明できる。
- 反応熱や状態変化によって出入りする熱の定義を言える。
(例:生成熱は化合物 $\pu{1 mol}$ がその成分元素の単体から生成するときに出入りする熱量のことである。) - 化学反応や状態変化による熱の出入りを熱化学方程式を用いて表現できる。
(例:水素と酸素から液体の水が $\ce{9.0 g}$ 生成するとき $\ce{143 kJ}$ の発熱があった。
このときの熱化学方程式は、水が $\pu{0.50 mol}$ できたことから $\f{\pu{143 kJ}}{\pu{0.50 mol}} = \pu{286 kJ/mol} $ であることに気をつけて、 $\ce{H2 (気) + \f{1}{2}O2(気) = H2O (液) + 286 kJ}$ と書ける。) - ヘスの法則が説明できる。
- 与えられた反応熱のデータから、求めたい反応熱の値が計算できる。
- 結合エネルギーの定義が言え、それに関わる問題が解ける。
- 化学発光や光合成の簡単な説明ができる。
化学反応の速さと化学平衡
- 反応速度の定義が言えて、計算問題が解ける。
- 反応速度を上げる $3$ つの要因、濃度・温度・触媒について説明できる。
- 化学反応が起こるしくみを、活性化状態に関連付けて説明できる。
- 気体の平衡定数や圧平衡定数を用いて種々の問題が解ける。
- ルシャトリエの原理を用いて外部の変化に対して平衡がどのように移動するか答えられる。
- 平衡の観点からハーバー・ボッシュ法について説明できる。
- 電離定数を使って弱酸や弱塩基の電離度や pH が計算できる。
- 水溶液の緩衝作用について酢酸と酢酸ナトリウムの混合液を使って説明できる。
また、緩衝液の pH が計算できる。 - 塩の水溶液について加水分解定数を使って pH が計算できる。
- 難溶性の塩の水溶液について、溶解度積を用いて種々の計算問題が解ける。



