- リチウムイオン電池がどのような電池なのか、概要を知りたい。
- 入試問題でどのように出題されているかを知りたい。
上記の知りたいに答えられるように15年間予備校講師を続けている著者が記事を書きました。
高校化学全体の勉強法やおすすめの参考書はコチラから読めます!
2019年10月 吉野彰 氏 らノーベル化学賞受賞
ニュースサイトより記事を引用します。
スウェーデンの王立科学アカデミーは9日、リチウムイオン電池の開発に寄与した3人にノーベル化学賞を贈ると発表した。リチウムイオン電池が「モバイルの世界を可能にした」と評価している。
米テキサス大学オースティン校のジョン・B・グッドイナフ教授(97)、ニューヨーク州立大学ビンガムトン校のM・スタンリー・ウィッティンガム教授(77)、そして日本の旭化成名誉フェローで名城大学教授の吉野彰氏(71)の3人。900万スウェーデンクローナ(約9700万円)の賞金は3人で分け合う。
グッドイナフ氏は、ノーベル賞受賞時の年齢としては史上最高齢。
リチウムイオン電池は軽く、再充電が可能な電池で、携帯電話やラップトップ、電気自動車(EV)などに利用されている。また、太陽光発電や風力発電といった再生可能エネルギーの蓄電にも活用されている。
BBC NEWS JAPAN
日本人がノーベル化学賞を受賞したのは9年ぶりのことです。
(2010年に鈴木章氏と根岸英一氏が、「クロスカップリング反応の研究」により受賞しています。)
私たちの生活の中では、スマートフォンやノートパソコンなどの電子機器が溢れています。
これらに使用される小型で安全なバッテリーとして、リチウムイオン電池の需要は依然として高いままです。
大学入試におけるリチウム電池の過去の出題例
2006京都大学

著者が持っているソフト 『 Studyaid D.B オンライン 』や『 Xam (イグザム)』でリチウムイオン電池と検索すると、
2014年、2016年、2018年 早稲田大学
2019年 岡山大学
2020年 金沢医科大学、日本大学、兵庫医科大学
など超頻出というわけではないですが、
難関大学を中心に出題されています。
日常的によく用いられている電池であるため、これからも出題はされていくでしょう。
リチウムイオン電池の内部の様子
大学入試問題では、イオン反応式が与えられて
その式をもとに計算をしていきます。
問題文中で、リチウムイオン電池がどのような反応をするかは書いてあることが多いですが、
事前に知識を少しでも入れておくとイメージしやすいです。
まずは、負極・正極それぞれがどのような反応をしているか見ておきましょう。
負極での反応
負極材料にはカーボン( $\ce{C}$ ) を用います。
炭素原子が層状になっていて、層と層の間に $\ce{Li^+}$ をとどめて置くことができます。

最大数の $\ce{Li^+}$ が炭素原子の層間に存在するとき、
炭素原子 $6$ 個につき $\ce{Li^+}$ $1$ 個の割合で配置されます。
これを組成式で $\mathbf{\color{red}{\ce{LiC6}}}$ と表現します。

層間の $\ce{Li^+}$ の数は最大数より少なければ任意です。
よって $0 < x \leqq 1$ である $x$ を用いて、 $\ce{Li_{x}C6}$ と書けます。
例えば $\ce{Li_{0.5}C6}$ の場合, $\ce{C}$ 原子 $12$ 個につき $\ce{Li}$ が $1$ 個の割合で存在することを意味します。
充電反応は、この層間に $\ce{Li^+}$ を入れる反応です。
$\ce{6C + xLi^+ + $x$e^- –> Li_{x}C6} \hspace{5mm} ( 0 < x \leqq 1) $
仮に層間に最大量の $\ce{Li+}$ が入るときは $x = 1$ なので、
$\ce{6C + Li^+ + e^- –> LiC6}$
と書けます。
正極での反応
正極材料にはコバルト酸リチウム ( $\ce{LiCoO2}$ ) を用います。
「コバルト原子と酸素原子による八面体構造」で形成された層とリチウム原子の層からなる物質です。
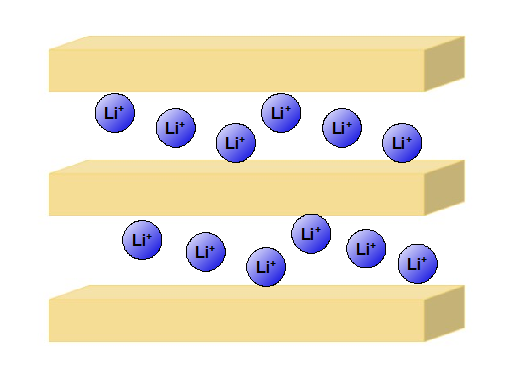
充電するときは、この層から $\ce{Li+}$ が抜けて、電解液を通って正極の炭素の層に入っていきます。
$\ce{LiCoO2 -> xLi+ + $x$e- + Li_{1-x}CoO2 } ( 0 < x \leqq 1) $
仮に全ての $\ce{Li+}$ が放出されるときは $x = 1$ なので、
$\ce{LiCoO2 -> Li+ + e- + CoO2 } $
と書けます。
このとき $\ce{Co}$ 原子の酸化数は、$+3 → +4 $ に変化しています。
リチウム電池全体としての反応
全体で見ると、$\ce{Li+}$ が、イオンのまま負極と正極の層間を行き来しているだけです。
電極は、電荷の分布状態や酸化数は変わりますが、構造自体は変化しません。
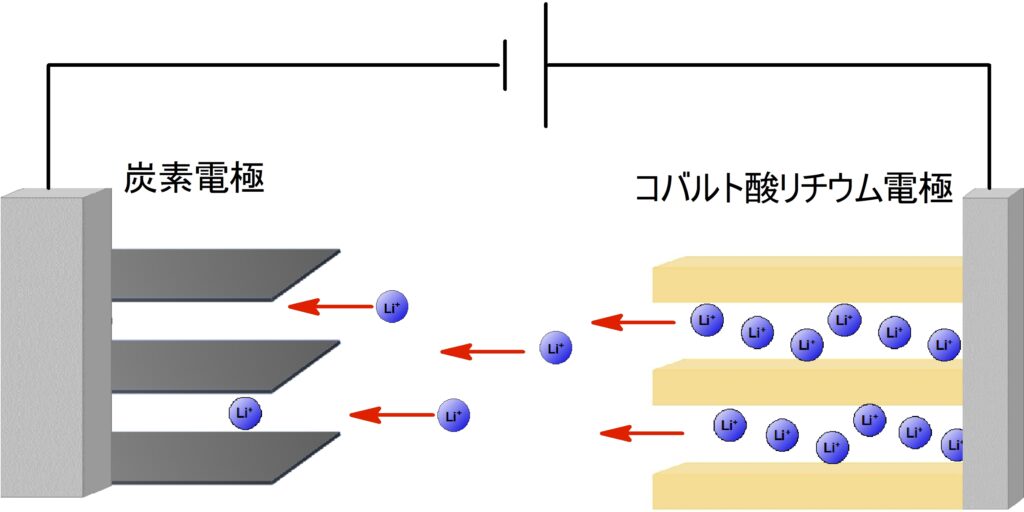
有機電解液中を $\ce{Li+}$ が移動する。
放電時は逆向きに移動する。
なお,完全に充電されるときに,
全ての $\ce{Li+}$ が移動するわけではない。
以下 $x$ を,$ ( 0 < x \leqq 1)$とする。
右向きの反応を充電反応、左向きの反応を放電反応として、
(負極)
$\ce{6C + xLi^+ + $x$e^- \rightleftarrows Li_{x}C6} \hspace{5mm}$
(正極)
$\ce{LiCoO2 \rightleftarrows xLi+ + $x$e- + Li_{1-x}CoO2 }$
各辺を足して $\ce{e-}$ を消去すると、
(全体)
$\ce{6C + LiCoO2 \rightleftarrows Li_{x}C6 + Li_{1-x}CoO2}$
特に $x=1$ のときは
(負極)
$\ce{6C + Li^+ + e^- \rightleftarrows LiC6} $
(正極)
$\ce{LiCoO2 \rightleftarrows Li+ + e- + CoO2 } $
各辺を足して $\ce{e-}$ を消去すると、
(全体)
$\ce{6C + LiCoO2 \rightleftarrows LiC6 + CoO2} $
リチウムイオン電池の計算問題の例題
リチウム二次電池を放電すると負極の質量は $\pu{2.30 g}$ 減少した。この質量変化から計算すると、流れた電子の物質量 [$\pu{mol}$] はいくらになるか。原子量は $\ce{Li}$ = 6.94 を用いよ。
また、リチウム二次電池の放電における負極の反応は次の式を用いよ。
$$\ce{Li_{x}C6 -> xLi^+ + 6C + $x$e^{-}}$$
負極のイオン反応式より
$\pu{1 mol}$ の $\ce{Li+}$ が抜けると、$\pu{1 mol}$ の $\ce{e^{-}}$ が流れるので
$$\displaystyle \frac{ 2.30 }{ 6.94 } \times 1 = 0.3314$$
ゆえに、$\pu{0.331 mol}$ が答えです。
充電されたあるリチウムイオン電池を充電すると、電源から $\pu{3.86E5 C}$ の電子が流れた。
負極の質量は、何 $\pu{g}$ 変化したか。有効数字 $2$ 桁で求めよ。
ファラデー定数は $\pu{9.65E4 C/mol}$、$\ce{Li}$ の原子量は $6.9$ を用いよ。
また、負極における充電の反応式は下の通りである。
$\ce{6C + xLi^+ + $x$e^- –> Li_{x}C6} \hspace{5mm} ( 0 < x \leqq 1) $
電源から流れた電子の物質量 [$\pu{mol}$] は、
$$\dfrac{\pu{3.86E5 C}}{\pu{9.65E4 C/mol}} = \pu{4.00 mol}$$
反応式より、$\pu{1 mol}$ の $\ce{e-}$ が流れると、$\pu{1 mol}$ の $\ce{Li+}$ が層に入るので、
求める値は、
$$\pu{4.00 mol} \times 1 \times \pu{6.9 g/mol} = \pu{27.6 g}$$
したがって $\bold{\pu{28 \bold{g}}}$ の増加が答えです。
リチウムイオン電池は正極と負極の充電容量(蓄えることのできる電気量)が正確に一致するように、それぞれの電極活物質の質量を決めて作られている。負極として黒鉛 ( $\ce{C}$ ) $\pu{1.44 g}$ を用いた場合、正極活物質として $\ce{LiCoO2}$ を何 $\pu{g}$ 用いれば、正極と負極の充電容量が等しくなるか。有効数字 $3$ 桁で求めよ。
ただし満充電のときに半数の $\ce{Li+}$ が正極に残っており、等量の $\ce{Li+}$ が移動したとして、次の充電反応のイオン反応式を用いよ。式量は $\ce{C} = 12.0, \ce{LiCoO2} = 98.0$ を用いよ。
(負極)
$\ce{6C + Li^+ + e^- –> LiC6}$
(正極)
$\ce{LiCoO2 -> 0.5Li+ + $0.5$e- + Li_{0.5}CoO2 } $
同じ電気量が蓄えられるので、$\ce{e-}$ の係数を揃えて足すと、
$\ce{6C + 2LiCoO2 ->[e-] LiC6 + 2Li_{0.5}CoO2}$
$\ce{C}$ と $\ce{LiCoO2}$ の係数比は $3 : 1$ であるから、物質量について、
$\dfrac{\pu{1.44 g}}{\pu{12 g/mol}} \times \dfrac{1}{3} = \dfrac{\pu{{w} g}}{\pu{98 g/mol}}$
したがって、$w = \pu{3.92 g}$ となります。




