[table id=6 column_widths=”10%|20%|10%|20%”/]
問１ 単結合のみをもつ物質
$\waku{1}$
単結合というのは、原子間をつなぐ 1 本の共有結合のことである。
$\,1\,$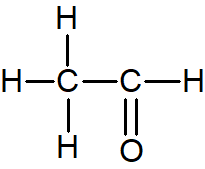 
二重結合を含むので不適。
$\,2\,$
三重結合を含むので不適。
$\,3\,$
$\ce{Br – Br}$ で単結合のみ。適。
$\,4\,$
$\ce{Ba}$ は金属元素、 $\ce{Cl}$ は非金属元素なのでこれらの間はイオン結合。不適。
問2 コロイドの分類
$\waku{2}$
流動性のあるコロイド溶液をゾルといい、冷却して流動性を失ったかたまりを (a) ゲル という。さらにこのゲルから水分を除去すると、(b) キセロゲル（乾燥ゲル） が生成する。
なお、エアロゾルは気体中に液体粒子がコロイドの大きさかそれ以上の大きさで分散しているものを指す。雲や霧が該当する。
問3 液化した水の量の計算
$\waku{3}$
圧縮前の $\ce{H2O}$について状態方程式を立てると、その物質量を $\pu{n [mol]}$ として
$\pu{3.0E3} \times 24.9 = nRT$ (1)
圧縮後の $\ce{H2O}$ について状態方程式を立てると、その気体の物質量を $\pu{n_g [mol]}$ として
$\pu{3.6E3 \times 8.3 = n_g RT}$ (2)
凝縮した $\ce{H2O}$ は $n-n_g$で表せるから、(1) – (2) を左辺・右辺それぞれで計算して、
$\pu{3.0E3} \times 24.9 – \pu{3.6E3} \times 8.3 = (n-n_g)RT$
$n-n_g = \dfrac{(\pu{9.0E3 – 3.6E3}) \times 8.3}{\pu{8.3E3} \times 300} = \dfrac{5.4}{300} = 0.018$
問4 イオン結晶（配位数・結晶の体積・限界半径比）
$\waku{4}$
イオン結晶の配位数は、異種の粒子が最大何個と接することができるかを示す数であることに注意。
図2左側の注目している正方形で確認すると、
$\ce{S^{2-}}$ は最も近い $\ce{Ca^{2+}}$ と上下左右前後の 6 個接している。
故に配位数は 6 。
$\ce{CaS}$ は $\ce{Ca^{2+}}$ と $\ce{S^{2-}}$ が $1:1$ で存在するので、
$\ce{Ca^{2+}}$の配位数も6。
$\waku{5}$
図の正方形の1辺の長さは、
$R_{\ce{S}} + 2r_{\ce{Ca}} + R_{\ce{S}} = 2(R_{\ce{S}} + r_{\ce{Ca}})$
これが単位格子の1辺の長さであるから$3$乗して、
$V = 8(R_{\ce{S}} + r_{\ce{Ca}})^3$
$\waku{6}$
増加した体積 $\pu{15 cm^3}$ は沈めた $\pu{40 g}$ 分の $\ce{CaS}$ の結晶の体積に対応する。
結晶は単位格子が繰り返してできたものであるから、
（単位格子1個の体積）$\times$（単位格子の個数）= $\pu{15 cm^3}$ (3)
が成り立つ。
$\ce{CaS}$の$\pu{40 g}$ は、$\dfrac{\pu{40 g}}{\pu{72 g/mol}} = \dfrac{5}{9} \pu{mol}$
単位格子中に $\ce{CaS}$は$4$個あるから、単位格子の個数は
$\dfrac{\dfrac{5}{9} \times \pu{6.0E23}}{4} = \dfrac{5}{6} \times \pu{E23}$
したがって、(3) 式より
（単位格子1個の体積）$\times (\dfrac{5}{6} \times \pu{E23}) = \pu{15 cm^3}$
（単位格子1個の体積）= $1.8 \times \pu{E-22}$
$\waku{7}, \waku{8}$
普通陰イオンの方が大きく、陽イオンの方が小さい。（図2の通りに考えると良い。）
図2の右側にある正方形について、その1辺の $\sqrt{2}$ 倍が対角線の長さとなる。
陰イオン（大きい方の粒子）どうしが接しているとき、
$4R = \sqrt{2} \times 2(R + r)$
$R = \dfrac{\sqrt{2}}{2-\sqrt{2}}r = (\sqrt{2} + 1)r$
R がこれ以上大きくなると陰イオンのみが接するので不安定である。
