第1問
(1) 鉄とチタンからなる水素吸蔵合金
(ア)
鉄の原子半径、チタンの原子半径、単位格子の 1 辺をそれぞれ、$r$, $R$, $l$ とおく。
図にある体心立方格子から考えると、鉄とチタンは立方体の体対角線で接していることから、
$2(r+R)=\sqrt{3}\ l$ が成立する。
$l = \dfrac{2\sqrt{3} (r+R)}{3}$
$r=0.124, R=0.146, \sqrt{3} = 1.73 $ を代入すると、
$l = 0.3114$
(答1) $\boldsymbol{\pu{0.311 (nm)}}$
※有理化せずに代入すると、
$l=0.3121 \cdots$ となり
(答2) $\boldsymbol{\pu{0.312 (nm)}}$
どちらでも可であろう。
(イ)(答)水素吸蔵合金 または 水素貯蔵合金
(ウ)
問題文より、$\ce{H}$ 原子は立方体の面心に位置することから
一つの単位格子に取り込まれる $\ce{H}$ 原子の最大数は、
$\dfrac{1}{2} \times 6 = 3$
(答)$\bold{3}$ (個)
(エ)
$\ce{H}$ 原子を取り込んだとき、$\ce{Fe}$, $\ce{Ti}$ のどちらと接しているのかを考察する。
(i) $\ce{Ti}$ と $\ce{H}$ が接している場合。
このときの単位格子の1辺を $L_1$ とおく。
$\dfrac{1}{\sqrt{2}}L_1 =0.146+0.037$
(右辺は $\ce{Ti}$ と $\ce{H}$ の原子間距離。)
$=0.183$
よって $L_1 = 0.258$
$\ce{Fe – H}$ 間距離の$2$倍と $L_1$ を比較すると、
$2\times(0.124+0.037) > 0.258(=L_1)$
$\ce{Fe – H}$ 間距離の$2$倍の値は単位格子の1辺を超えられないので、これは不適。
この地点で次の (ii) が適するということで話を進めても良いが、一応確認する。
(ii) $\ce{Fe}$ と $\ce{H}$ が接している場合。
このときの単位格子の1辺を $L_2$ とおく。
$\dfrac{L}{2}=0.124+0.037$
(右辺は $\ce{Fe}$ と $\ce{H}$ の原子間距離。)
$=0.161$
よって $L_2=0.322$
$\ce{Ti – H}$ 間距離の $2$ 倍と $\sqrt{2}\, L_2$ を比較すると、
$2\times(0.146+0.037) < 1.41\times 0.322(=\sqrt{2}\, L_2)$
( $0.366<0.454$ となる。)
であるから、$\ce{Ti-H}$ は単位格子の中で存在できている。($\ce{Ti – H}$ 間距離の$\,2\,$倍の方が小さいので、$\ce{Ti – H}$ は接していない状態である。)
(i)(ii) より $\ce{Fe-H}$ が接している場合の $L_2$ が適なので
(答) $\boldsymbol{\pu{0.322 nm}}$
(オ)
$\ce{FeTiH}$ 1 個あたり、$\ce{H}$ 原子が 1 個存在する。
$\dfrac{\pu{6.19 g/cm^3} \times \pu{1000 cm^3}}{\pu{55.8 + 47.9 +1.00 (g/mol)}} \times 1 \times (6.02 \times 10^{23})$
$= \pu{59.12 mol} \times (6.02 \times 10^{23})$
$= 3.559 \times 10^{25}$
(答) $\bold{3.56 \times 10^{25}}$ 個
(カ)
前問より $\ce{H}$ 原子は $\pu{59.12 mol} $ であるから、
$\ce{H2}$ 分子は $\pu{\dfrac{59.12}{2} mol} = \pu{29.56 mol} $
気体の状態方程式より、
$V = \dfrac{nRT}{P}$
$= \dfrac{29.56 \times (8.31 \times 10^3 \times 298)}{1.00 \times 10^6}$
$= 73201 \times 10^{-3}$
(答)$\boldsymbol{\pu{73.2 L}}$
(キ)
穴埋めの雰囲気的に、「超臨界流体」が埋められるだろう。
前問と本問の条件で気体の状態方程式を並べると、
前問 $(1.00 \times 10^6) \times 73.2 = nRT$
本問 $P \times 1.00 = nRT$
( $P$ は密閉容器内の圧力である。 )
この2式を連立すると、
$P = \pu{73.2 \times 10^6 Pa}$ となり、
このときの温度は $\pu{298 K}$ である。
気体と液体の密度が等しい点 = 臨界点が $\pu{33.2 K}, \pu{1.22E6 Pa}$だから、
明らかに本条件は温度・圧力が臨界点を超えている。
ゆえに超臨界流体となっていることが分かる。
(2) 溶解熱による温度上昇、Naの周辺
(ク)
溶解熱によって温度が $\pu{T [K]}$ 上昇したとすると、
ゆえに溶液の温度は
$298 + 2.500 = 300.5$
(答) $\boldsymbol{\pu{301 K}}$
(ケ) 潮解
(コ) $\bold{\ce{Na2CO3}}$
(サ) $\bold{\ce{NaHCO3}}$
$\ce{NaOH}$ は大気中に体積で約 $0.04$ % 含まれる気体 A = $\ce{CO2}$ を吸収して
$\ce{2NaOH + CO2 -> Na2CO3 + 2H2O}$
の反応により $\ce{Na2CO3}$ を生成する。この物質は、
$\ce{2NaHCO3 -> Na2CO3 + H2O + CO2}$
の熱分解反応で得られる。
第2問
(1) ヨウ素
(ア)(答)O (イ)(答)$\bold{7}$
$\ce{I}$ は第5周期に属するため、最外殻電子は (K, L ・・・と数えて) O 殻に存在する。
また、$17$族であるから、最外殻電子数は $7$ 個である。
(ウ)(答)ファンデルワールス力 または 分子間力
ヨウ素は分子結晶。構成粒子である分子どうしが弱い引力によって結晶をつくっている。
この引力は分子間力である。
分子間力とはファンデルワールス力と水素結合の総称であり、
ヨウ素の結晶には水素結合が存在しないため、ファンデルワールス力がより良い答えとなる。
(2) KI水溶液の電気分解
(エ)
陰極に流れた電子の物質量は、
$\dfrac{\pu{0.500 A} \times \pu{5790 s}}{\pu{9.65E4 C/mol}} = \pu{0.0300 mol}$
陰極におけるイオン反応式は
$\ce{2H2O + 2e- -> H2 + 2OH-}$
したがって、生成する $\ce{H2}$ は、
$\pu{0.0300 mol} \times \dfrac{1}{2} = \pu{0.0150 mol}$
(答)$\boldsymbol{\pu{1.50E{-2} mol}}$
(オ)(答)$\bold{\ce{I3^{-}}}$
陽極では
$\ce{2I- -> I2 + 2e-}$
の反応によりヨウ素が生じるが、溶液中の $\ce{I-}$ と
$\ce{I2 + I- -> I3-}$
のように反応して三ヨウ化物イオンを生じる。
(カ)(答)デンプン
生成したヨウ素をチオ硫酸ナトリウムで滴定している。
終点付近で水溶液の色が青紫色から無色に変化した、という文章と合わせて考えると、
指示薬にデンプン水溶液を用いたことが分かる。
(キ)陽極のイオン反応式により、生成した $\ce{I2}$ は、
$\pu{0.300 mol} \times \dfrac{1}{2} = \pu{1.50E{-2} mol}$
$\pu{100 mL}$ 水溶液から、$\pu{50 mL}$ に取り出しているため、
この中には、
$\pu{1.50E{-2} mol} \times \dfrac{\pu{50 mL}}{\pu{100 mL}} = \pu{0.750E{-2} mol}$
のヨウ素分子が含まれている。
したがって、滴下したチオ硫酸ナトリウムの体積を $\pu{v [mL]}$ とおくと、
$\ce{I2 + 2e- -> 2I-}$
$\ce{2S2O3^{2-} -> S4O6^{2-} + 2e-}$
$\pu{1 mol/L \times \pu{\dfrac{v}{1000} L} \times 1= \pu{0.750E{-2} mol} \times 2}$
$\pu{v} = \pu{15 mL}$
(答) $\boldsymbol{\pu{15.0 mL}}$
(3) ヨウ化水素の平衡反応
(ク)
$\ce{H2 + I2 \rightleftarrows 2HI}$
$100$秒後 $\ce{HI}$ が $\pu{0.400 mol}$ 生成したので、
$\ce{H2}$ と $\ce{I2}$ はその半分量である $\pu{0.200 mol}$ 反応している。
故に、$\ce{[H2]}$ の平均減少速度は、
$v = \dfrac{\Delta [\ce{H2}]}{\Delta t} = \dfrac{\dfrac{\pu{0.200 mol}}{\pu{5.00 L}}}{\pu{100 s}}$
$= \dfrac{0.0400}{100}$
(答) $\boldsymbol{\pu{4.00E{-4} mol/L.s}}$
(ケ)
反応速度式 $v_1 = k_1 [\ce{H2}][\ce{I2}]$ を適用する。
問題文によると、$v_1$ はヨウ化水素の生成速度と定義されているので、
(ク)の 水素の減少速度 $v$ をそのまま用いてはならない。
反応式の係数比は、(反応量の mol 比に等しいことから)反応速度比に等しいので、
$v_1 = 2v = 2\times4.00\times10^{-4} = 8.00\times10^{-4}$
また、(ク)の反応速度は、$0$ 秒から $100$ 秒の平均値なので、モル濃度も平均値を用いる。
$8.00 \times 10^{-4} = k_1 \times \dfrac{\pu{0.500 mol}}{\pu{5.00 L}} \times \dfrac{\pu{0.500 mol}}{\pu{5.00 L}}$
$k_1 = 8.00 \times 10^{-2}$
(答) $\boldsymbol{\pu{8.00E{-2} L/mol.s}}$
(コ)
$\ce{H2 + I2 \rightleftarrows 2HI}$
平衡時、 $\ce{HI}$ が $\pu{1.02 mol}$ 生成したので、
$\ce{H2}$ と $\ce{I2}$ はその半分量である $\pu{0.510 mol}$ 反応している。
故に平衡時、$\ce{H2}$ と $\ce{I2}$ は
$\pu{0.600 mol}-\pu{0.51 mol}=\pu{0.0900 mol}$ 存在している。
したがって平衡定数は(分母と分子の次数が同じため、体積で割るのを省略して・・・)
$K = \dfrac{1.02^2}{0.0900 \times 0.0900} = 128.4 \cdots$
(答)$\bold{1.28 \times 10^2}$
(サ)
アレニウスの式 $k = Ae^{-\frac{E_a}{RT}}$ において自然対数をとると、
$\log_e k = -\dfrac{E_a}{R} \times T^{-1} + \log_e A$
$\pu{667 K}, \pu{714 K}$ の時の値を、表を用いて式に代入すると、
$2.75 = -\dfrac{E_a}{R} \times (1.50 \times 10^{-3}) + \log_e A$
$4.85 = -\dfrac{E_a}{R} \times (1.40 \times 10^{-3}) + \log_e A$
下の式から上の式を辺々引くと、
$2.10 = \dfrac{E_a}{R} \times 0.10 \times 10^{-3}$
この式に $R = \pu{8.3 J/mol} = \pu{8.3E{-3} kJ/mol}$ を代入して計算。
(答)$\boldsymbol{\pu{1.74E2 kJ/mol}}$
第3問
(1) スチレンの周辺
化合物 A について
・分子量が $102$
・炭素と水素のみからなる。
・環状構造はベンゼン環のみ。
・水素が付加可能。
・水素を付加させると、熱可塑性樹脂の単量体となる化合物 B が生成。
特に一番下の条件からベンゼン環をもつ単量体を考えていくと分かりやすい。
水素付加が可能なので、$\ce{C=C}$ や $\ce{C≡C}$ の存在を疑う。
またベンゼンの分子量が $78$ なので、置換基の分子量は $34$ 前後。置換基の炭素数が$2$個くらいだろうとあたりをつければ、化合物 B はスチレンと推測できる。分子量は $104$ で $102+2$ (=$\ce{H2}$ の分子量)で辻褄が合う。
したがって、化合物 A は側鎖の炭素間に三重結合をもつ構造式が考えられる。
(答)(ア)
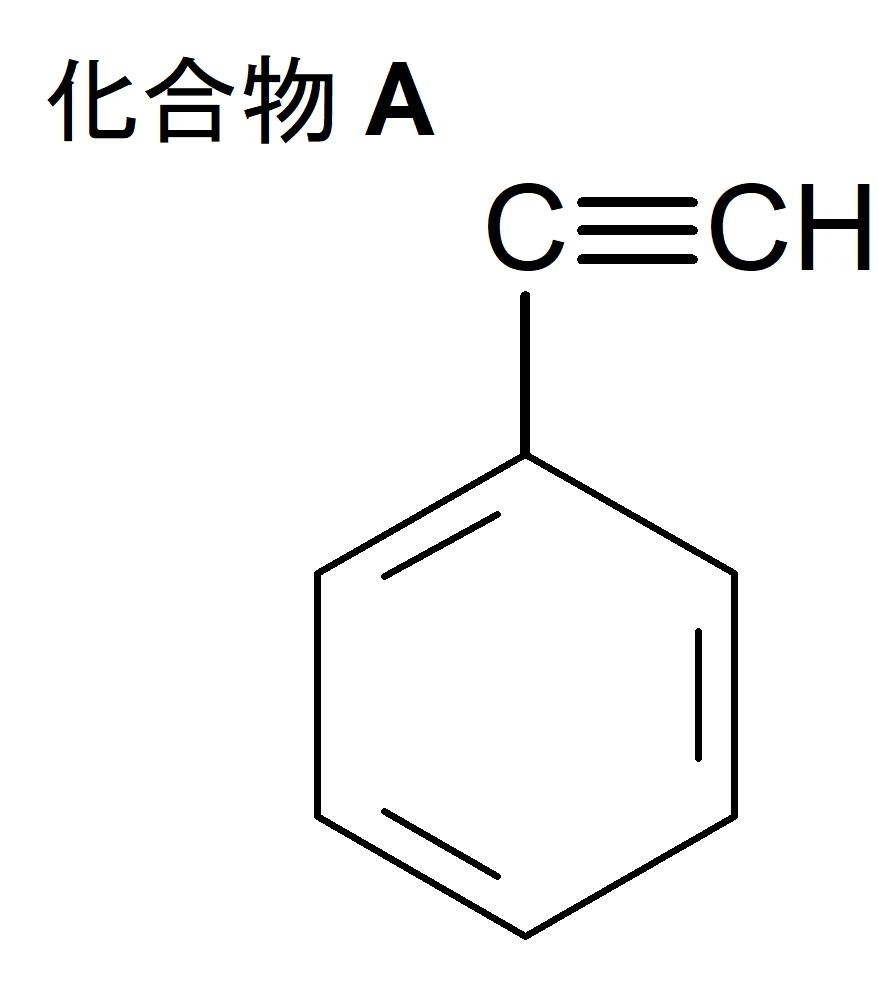
(イ) スチレン
(ウ)$\pu{1.0 mol}$ の A に対して、$\ce{Br2}$ は $\pu{2.0 mol}$ 反応できる。 (答)$\bold{\pu{2.0 mol}}$
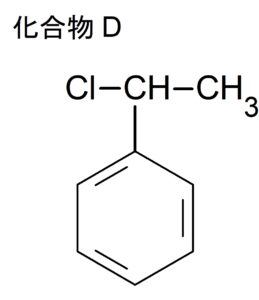
(エ)スチレンの炭素間二重結合に対して $\ce{HCl}$ を付加させる。
主生成物を答えるのでマルコフニコフ則を適用する。
より $\ce{H}$ 原子が多く結合している $\ce{C}$ 原子に $\ce{HCl}$ の $\ce{H}$ 原子を付加させれば良い。
(2) 糖と芳香族化合物を構成成分に持つ物質の構造決定
(オ)
化合物 E について、
$\ce{C} : 924 \times \dfrac{12}{44} = 252 (\pu{ mg})$
$\ce{H} : 270 \times \dfrac{2}{18} = 30 (\pu{ mg})$
$\ce{O} : 450-282=168 (\pu{ mg})$
よって
$\ce{C} : \ce{H} : \ce{O} = \dfrac{252}{12} : 30 : \dfrac{168}{16}$
$= 2 : 2.85 : 1$
分子式を$(\ce{C2H_{2.85}O})_n$ とおくと、分子量が $300$ であることから、
$42.85n = 300$
$n = 7.001 \cdots$
したがって分子式は $n=7$ を代入して
(答)$\bold{\ce{C14H20O7}}$
(カ)
化合物 F は、セロビオースの加水分解生成物なのでグルコース(分子量 $180$)である。
芳香族化合物 G の分子量は、
(化合物 E の分子量)+ (水の分子量)- (糖化合物 F の分子量)
$= 300+18-180$
(答)$\bold{138}$
(キ)
化合物 G について
塩化鉄(III)水溶液が呈色したので、フェノール性ヒドロキシ基を持つ。
フェノールの分子量は $94$ で、脱水可能であることからオルトの二置換体であることを考慮すると、
ベンゼン環の$\ce{H}$ を1つ抜いて、確定している式量は $93$
化合物 G の分子量は $138$ であったから、残る部分の式量は
$138-93=45$
酸化・脱水後の化合物が五員環であることから、 $\ce{-COOH}$ 1つは不適。
フェノールの側鎖に $\ce{- CH2 – CH2 – OH}$ とすると式量 $45$ に合致する。
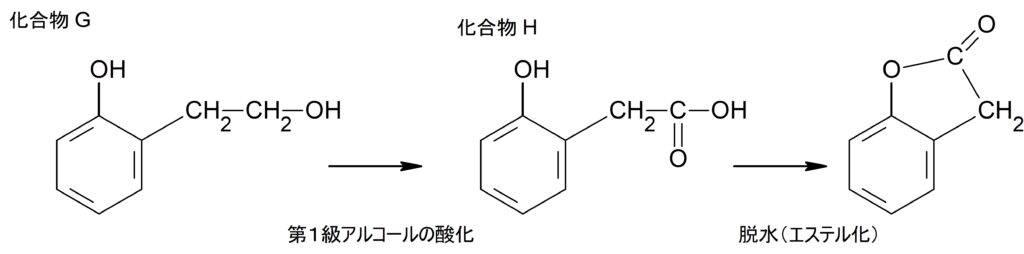
したがって(キ)はこの画像の一番左の構造を答えれば良い。
(ク)
化合物 E は塩化鉄(III)水溶液で呈色しないので、フェノール性ヒドロキシ基が糖化合物 F であるグルコースと $\beta -$ グリコシド結合をしている。答えは下の通り。
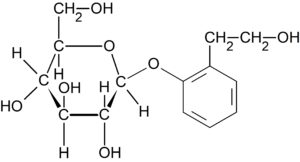
(3) ジペプチドの構造決定
(ケ)
化合物 J について
分子式が $\ce{C4H9NO3}$ で、$\alpha – $ アミノ酸の側鎖以外の化学式が $\ce{C2H4NO2}$ であるから、
側鎖は $\ce{C2H5O}$
化合物 J がヨードホルム反応を示すことから、下のトレオニンに決定する。
これが(ケ)の(答)
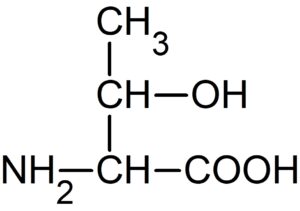
(コ)(答)システイン
化合物 K は酢酸鉛(II) で黒色沈殿を生じることから、 $\ce{S}$ が存在することが分かる。
この地点でシステインかメチオニンかは不明だが、
問題文の最後の行に側鎖が関わる結合とあるので、ジスルフィド結合が該当し、
K はシステインに決定する。(メチオニンは $\ce{- SH}$ を持たないため、ジスルフィド結合をしない。)
(サ) (答) $\boldsymbol{\beta -} $シート
二次構造でひだ状構造といえば、$\beta-$ シートである。
(シ)(答)ジスルフィド



