気体が水に溶けるときの計算問題がよく分からない。
「ヘンリーの法則を用いよ」と言われても、どう使うのかが分からない。
体積が絡んだ問題で答えが合わないことがある。
この記事ではヘンリーの法則を解説します。
公式の説明だけではなく、実際の問題を通して解法を載せるので、
読んでいけばきっと上記の悩みが解決に向かうでしょう。
高校化学全体の勉強法やおすすめの参考書はコチラから読めます!
ヘンリーの法則の基本の公式|水に溶けるモルは圧力と溶媒量に比例する
以下、溶媒は全て水で説明します。
水に溶けにくい気体において温度が一定であれば、水に溶ける気体の物質量$\,\pu{mol}\,$や質量$\,\pu{g}\,$は圧力に比例する。
このままでは実用性がないので、水の量を加味した形で理解しておくと良いです。
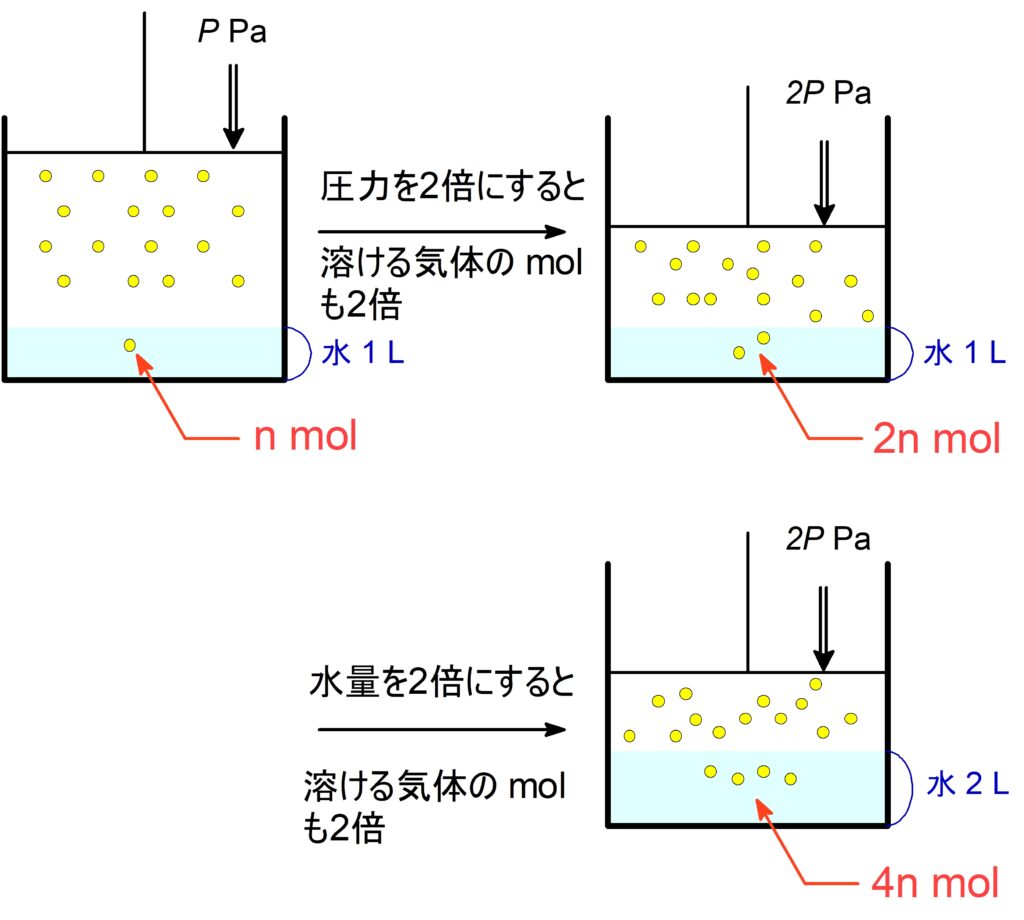
水に溶けにくい気体において、温度が一定であれば、水に溶ける気体の物質量$\,\pu{mol}\,$や質量$\,\pu{g}\,$は圧力や溶かしている溶媒量に比例する。
$\pu{P_{0} [Pa]}$ で水 $\pu{V_{0} [L]}$ に気体が $\pu{n_{0} [mol]}$ 溶けるとき、
$\pu{P_{1} [Pa]}$ で水 $\pu{V_{1} [L]}$ に溶ける気体の物質量 $\pu{n [mol]}$ は、
$\bold{\textcolor{red}{n = n_0\ \x\ \f{P_1}{P_0}\ \x\ \f{V_1\ \text{水}}{V_0\ \text{水}}}}$ で計算できる。

溶解する気体の mol は,その倍率に応じて変化する。
ヘンリーの法則の基本問題の解法
レベル1 | ヘンリーの法則の基礎
$0$ ℃, $\pu{1.0E5 \tume Pa}\,$の$\,\ce{N2}\,$は水$\,\pu{1.0 \tume L}\,$に$\,\pu{1.0E-3 \tume mol}\,$溶けるものとする。
今、$0$ ℃, $\pu{3.0E5 \tume Pa}\,$の$\,\ce{N2}\,$が水$\,\pu{2.0 \tume L}\,$に接している。有効数字は$\,2\,$桁で求めよ。
(1) この水に溶けている$\,\ce{N2}\,$は何$\,\pu{mol}\,$か。
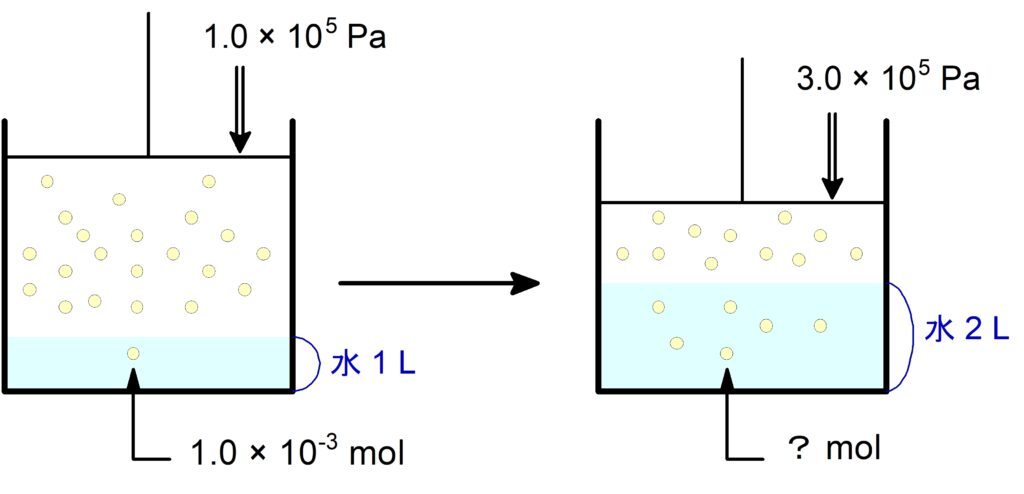
圧力を$\,3\,$倍かけて水を$\,2\,$倍にしたので、元の$\,\pu{mol}\,$より$\,6\,$倍溶けることになります。
それをきちんと式で表そうとしたら、公式の形になります。
答えは $\pu{6.0E-3 mol}$ です。
(2) この水に溶けている$\,\ce{N2}\,$の質量は何$\,\pu{g}\,$か。(分子量は$\,\ce{N2} = 28$ )
(1)の水に溶けている$\,\pu{mol}\,$を$\,\pu{g}\,$に直します。
$$\pu{6.0E-3 mol}\ \x\ \pu{28 g/mol} = \pu{168E-3 g}$$
(1) が聞かれていなくて,いきなり(2)を聞かれた場合は、$\pu{mol}\,$を出してから分子量をかければOKです。
有効数字$\,2\,$桁に直して、答えは $\pu{0.17 g}$ です。
(3) この水に溶けている$\,\ce{N2}\,$の体積は標準状態で何$\,\pu{L}\,$か。
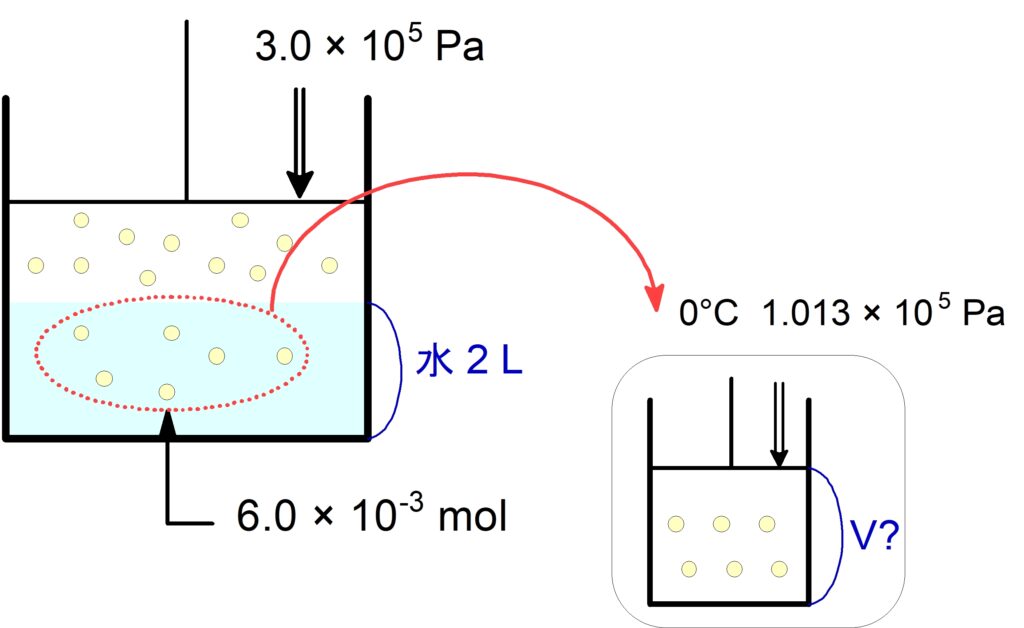
気体の体積を測るときは,圧力$\,P\,$, 温度$\,T\,$を指定する必要があります。
この作業は,水に溶けている気体を一旦とりだして,圧力$\,\bold{P}\,$・温度$\,\bold{T}\,$を指定した部屋で体積$\,\bold{V}\,$を測定すると考えると良いです。
(1)の水に溶けている$\,\pu{mol}\,$を標準状態での$\,\pu{L}\,$に直します。
$$\pu{6.0E-3 mol}\ \x\ \pu{22.4 L/mol} = \pu{133.4E-3 L}$$
(1)が聞かれていなくて,いきなり(3)を聞かれた場合は、$\pu{mol}\,$を出してから$\,22.4\,$をかければ OK です。
有効数字$\,2\,$桁に直して、$\pu{0.13 \tume L}\,$が答えです。
レベル2 | 体積が与えられたときのヘンリーの法則
$0$ ℃, $\pu{1.0E5 \tume Pa}\,$の$\,\ce{N2}\,$が水$\,\pu{1.0 \tume L}\,$に溶ける量は、標準状態に換算して$\,\pu{23 \tume mL}\,$である。今、$0$ ℃, $\pu{2.0E5 \tume Pa}\,$の$\,\ce{N2}\,$が水$\,\pu{1.0 \tume L}\,$に接している。有効数字は$\,2\,$桁で求めよ。
(1) この水に溶けている $\ce{N2}$ は何$\mathrm{\ mol}$ か。
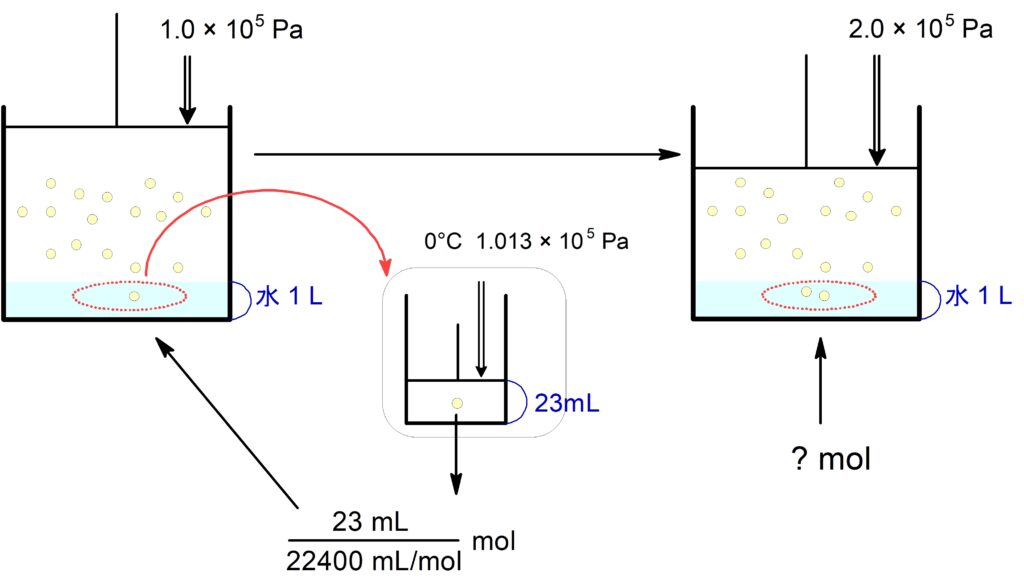
標準状態での $\pu{23 mL}$ を$\,\pu{mol}\,$に直しますが,その$\,\pu{mol}\,$は $\pu{1.0E5 Pa}$ かけていた時に水に溶けている$\,\pu{mol}\,$の値に等しいです。そこからヘンリーの法則を適用します。
この流れはしっかり理解しておきましょう。
(2)この水に溶けている$\,\ce{N2}\,$は標準状態で何$\,\pu{mL}\,$か。
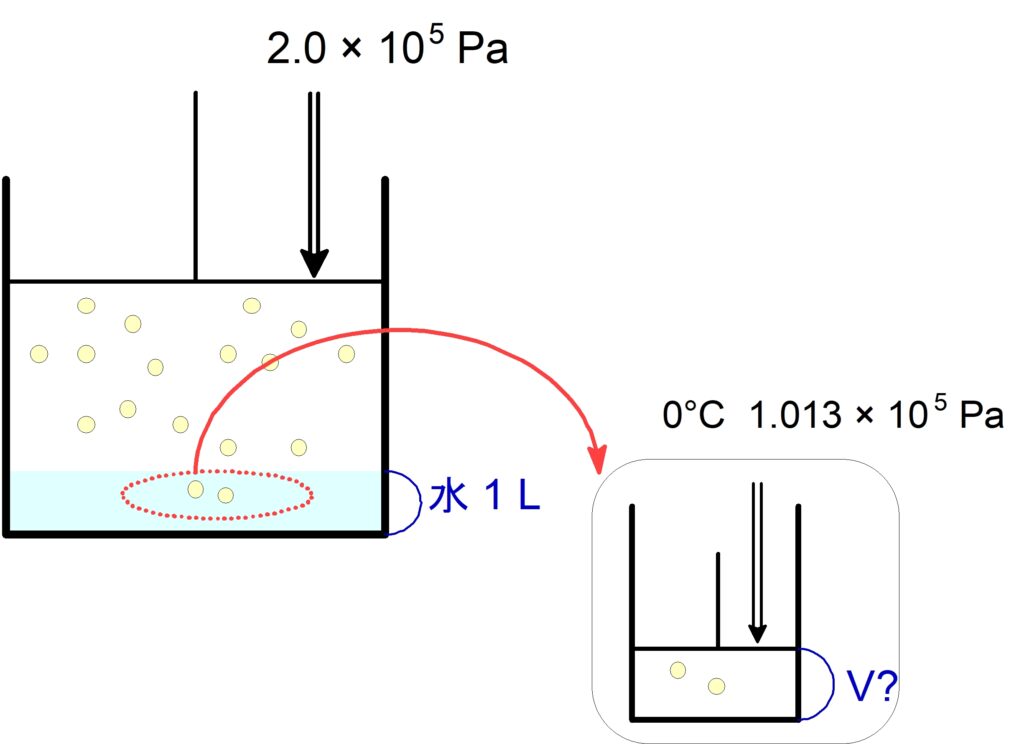
(3) この水に溶けている $\ce{N2}$ は、$0$ ℃, $2.0 \times 10^5 \mathrm{\ Pa}$ で何 $\pu{mL}$ か。
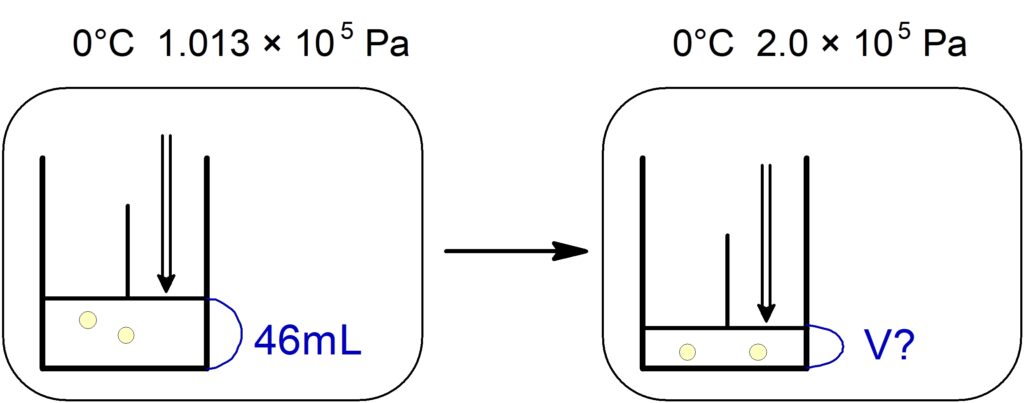
【解法1】(2)の利用
ボイル・シャルルの法則を用いて
\dfrac{PV}{T} &= \dfrac{P’V’}{T’} \\
\\
\dfrac{1.013 \times 10^5\ \mathrm{Pa}\ \times 46\ \mathrm{mL}\ }{273\ \mathrm{K}\ } &= \dfrac{2.0 \times 10^5\ \mathrm{Pa}\ \times V’\ \mathrm{mL}\ }{273\ \mathrm{K}\ } \\
\\
V’ & \fallingdotseq 23\ \mathrm{mL}\
\end{align}$
ヘンリーの法則のもう1つの公式|体積のみで考える問題
問題文中で水に溶ける気体の量が体積で与えられ、求める値も体積で答える場合、
次のように体積のみで考えると良いです。
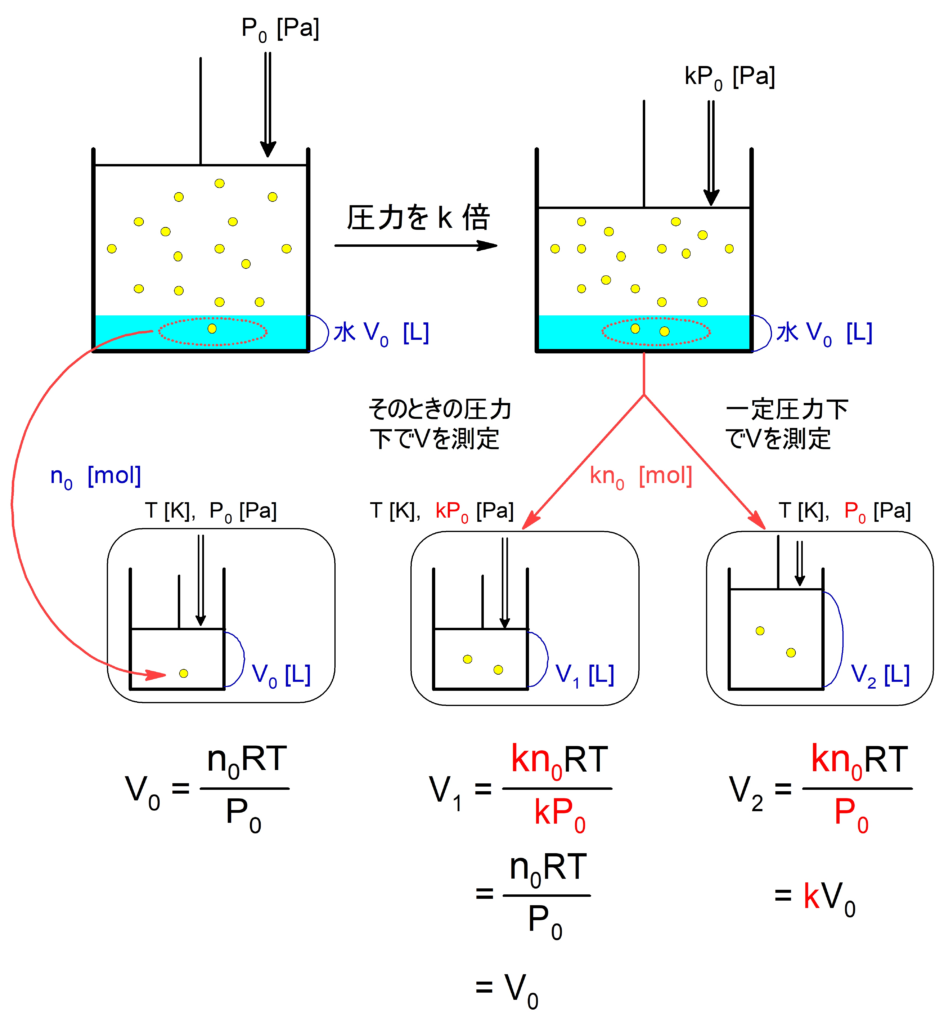
水に溶けにくい気体において、温度が一定であれば、水に溶ける気体の体積 ($\pu{L}$) について次のことがいえる。
(当記事では、体積ヘンリーと呼ぶことにする。)
・ そのときの圧力で体積をはかると、かけた圧力に依らず体積の値は一定である。
(ただし、水量や温度には比例する。)
$ \pu{V} = \pu{V_{0}}\ \x\ \f{V_1\ \text{水} }{V_0\ \text{水}}$
※ 圧力の倍率は不要!
・ 一定圧力下で体積をはかると、圧力に比例する。
(水量や温度にも比例する。)
$ \pu{V} = \pu{V_{0}}\ \x\ \f{P_1}{P_0}\ \x\ \f{V_1\ \text{水} }{V_0\ \text{水}}$
前の問題の (3) を、この考え方を使って解いてみよう。
(再掲)
$0\pu{℃}$, $1.0 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{N2}\,$が水 $1.0 \mathrm{\ L}$ に溶ける量は、標準状態に換算して $23 \mathrm{\ mL}$ である。今、$0$ ℃, $2.0 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{N2}\,$が水 $1.0 \mathrm{\ L}$ に接している。
(3) この水に溶けている$\,\ce{N2}\,$は、$0$ ℃, $2.0 \times 10^5 \mathrm{\ Pa}$ で何 $\pu{mL}$ か。
$\pu{2.0E5 Pa}$ で水に接している窒素の体積を、$\pu{2.0E5 Pa}$ の元で測るので、『そのときの圧力』で測っていることになります。
【解法2】いわゆる体積ヘンリーを用います。
そのときの圧力で水に溶けている気体の体積$\,V\,$を測定すると、圧力に依らず$\,V\,$は一定。
問題文中のデータにおいて $\pu{1.0 L}$ の水に溶ける$\,\ce{N2}\,$は $\pu{23 mL}$ とあるから、
水の倍率のみを考えて、
$23\ \mathrm{mL}\ \times \dfrac{1.0\ \mathrm{L\ \text{水}}}{1.0\ \mathrm{L\ \text{水}}} = 23\ \mathrm{(mL)}\ $
念のためもう$\,1\,$問、体積ヘンリーの問題を挙げておきます。
$0$ ℃, $1.0 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{O2}\,$が水 $1.0 \mathrm{\ L}$ に溶ける量は、標準状態に換算して $49 \mathrm{\ mL}$ である。今、$0$ ℃, $3.0 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{O2}\,$が水 $2.0 \mathrm{\ L}$ に接している。水に溶けている$\,\ce{O2}\,$の体積はこの時の温度・圧力において何$\ \mathrm{mL}\ $か。有効数字は$\,2\,$桁で求めよ。
そのときの圧力で水に溶けている気体の体積$\,V\,$を測定すると、圧力に依らず$\,V\,$は一定であるから、
水の倍率のみ考えて、
$$ 49\ \mathrm{mL}\ \times \dfrac{2.0\ \mathrm{L\ \text{水}}}{1.0\ \mathrm{L\ \text{水}}} = 98\ \mathrm{mL}\ $$
レベル3 | 混合気体(空気)のヘンリーの法則は分圧で考える
$0$ ℃, $1.0 \times 10^5 \mathrm{\ Pa}$ で $\ce{N2}$ と $\ce{O2}$ が水 $1.0 \mathrm{\ L}$ に溶ける量は、それぞれ標準状態に換算して $23 \mathrm{\ mL}, 49 \mathrm{\ mL}$ である。今、$0$ ℃, $1.0 \times 10^5 \mathrm{\ Pa}$ の空気が水に接している。水に溶けている$\,\ce{N2}\,$と$\,\ce{O2}\,$の物質量比(モル比)を最も簡単な整数比で答えよ。ただし空気に含まれる$\,\ce{N2}\,$と$\,\ce{O2}\,$の物質量比(モル比)を$\,4:1\,$とする。
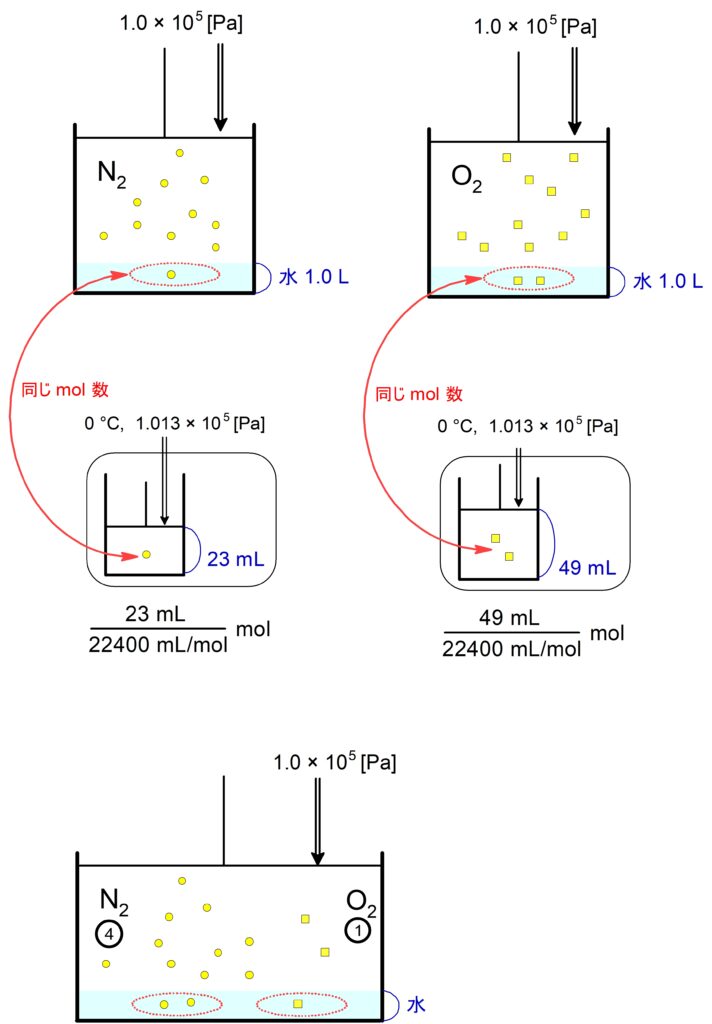

水の量を $v \ \mathrm{L}\ $とすると
\dfrac{ \ce{N2} }{ \ce{O2} }
&= \dfrac{ \dfrac{23\ \mathrm{mL}\ }{22400\ \mathrm{mL/mol}\ } \times \dfrac{1.0 \times 10^5 \times \dfrac{4}{5} \ \mathrm{Pa}\ }{1.0 \times 10^5 \ \mathrm{Pa}\ } \times \dfrac{v \ \mathrm{L\ \text{水}}\ }{1\ \mathrm{L\ \text{水}}\ } }{\dfrac{49\ \mathrm{mL}\ }{22400\ \mathrm{mL/mol}\ } \times \dfrac{1.0 \times 10^5 \times \dfrac{1}{5} \ \mathrm{Pa}\ }{1.0 \times 10^5 \ \mathrm{Pa}\ } \times \dfrac{v \ \mathrm{L\ \text{水}}\ }{1\ \mathrm{L\ \text{水}}\ } } \\
\\
&= \dfrac{23 \times 4}{49}\\
\\
&= \dfrac{92}{49}
\end{align}$$
したがって、$ \ce{N2} : \ce{O2} = 92 : 49$
レベル4 | 温度変化を考慮するヘンリーの法則
$40$ ℃, $1.013 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{N2}\,$が水 $1.0 \mathrm{\ L}$ に溶ける量は、標準状態に換算して $11.6 \mathrm{\ mL}$ である。今、$40$ ℃, $2.026 \times 10^5 \mathrm{\ Pa}$ の$\,\ce{N2}\,$ が水 $1.0 \mathrm{\ L}$ に接している。
(1) この水に溶けている$\,\ce{N2}\,$の体積は標準状態で何$\ \mathrm{mL}\ $か。有効数字は$\,2\,$桁で求めよ。
有効数字$\,2\,$桁に直して、答えは $23\mathrm{\ mL}$ です。
(2) この水に溶けている$\,\ce{N2}\,$の体積は、$40$ ℃, $2.026 \times 10^5 \mathrm{\ Pa}$で何$\ \mathrm{mL}\ $か。
【解法1】体積ヘンリーを用いる
そのときの圧力で水に溶けている気体の体積$\,V\,$を測定すると、圧力に依らず$\,V\,$は一定。
問題文中のデータの体積 $11.6\ \mathrm{mL}\ $は標準状態($0$ ℃)、調べたい体積は$\,40\,$℃ なので、温度変化があることに注意しましょう。
$\,PV=nRT\,$において、$P, n, R\,$が一定だから、$\,V\,$は$\,T\,$に比例します。
有効数字$\,2\,$桁に直して、答えは $13\mathrm{\ mL}$ です。
【解法2】(1)の結果を用いる
(1)の体積は標準状態なので、
調べたい環境は、
これらよりボイル・シャルルの法則を用いると、
= \dfrac{2.026 \times 10^5\ \mathrm{Pa}\ \times V’\ \mathrm{mL}\ }{313\ \mathrm{K}\ }$$
有効数字$\,2\,$桁に直して、答えは $\pu{13 mL}$ です。
レベル5−1 | 定積容器におけるヘンリーの法則は気相と液相に分けて立式
$\pu{40 ℃}$, $\pu{1.013E5 Pa}$ の$\,\ce{N2}\,$が水 $\pu{1.0 L}$ に溶ける量は,標準状態に換算して $\pu{11.6 mL}$ である。いま,中を真空にした容積 $\pu{1.86 L}$ の密閉容器に水 $\pu{200 mL}$ を入れた後,$\pu{0.56 g}$ の$\,\ce{N2}\,$を入れて $\pu{40 ℃}$ に保ったまま十分に放置した。水中に溶けている$\,\ce{N2}\,$の物質量 [$\mathrm{mol}$] はいくらか。有効数字$\,2\,$桁で答えよ。$\,\ce{N}\,$の原子量は$\,14\,$, 気体定数は $\pu{8.3E3 Pa*L / (K*mol)}$ を用い,容器内の水は蒸発しないものとする。
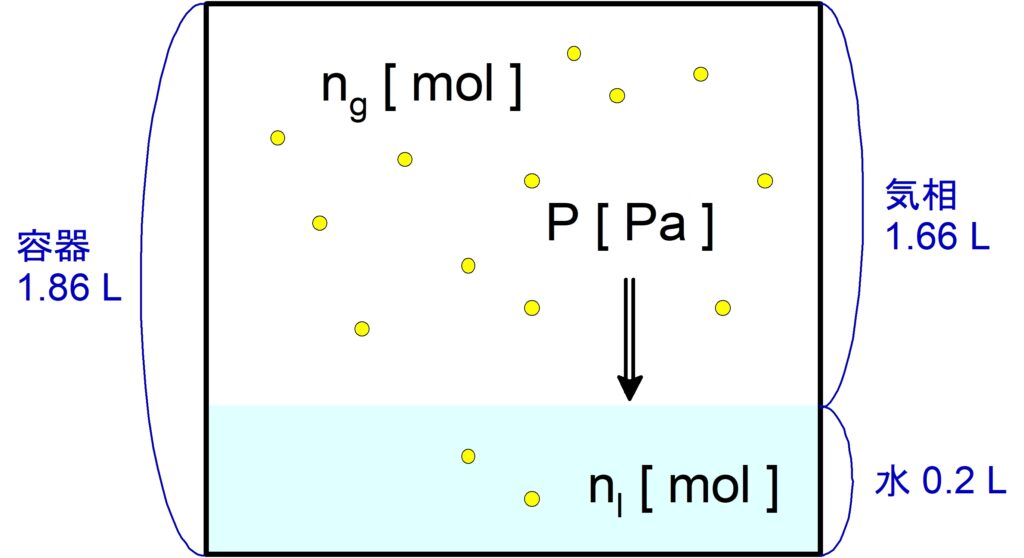

気相(気体のみの部分)では$\,\bold{PV = nRT}\,$、液相(液体の部分)ではヘンリーの法則をそれぞれ適用して連立します。
気相について
気体の体積$\,V\,$は気体粒子が動き回れる範囲なので,水の体積分を引く必要があります。
$V = \pu{1.86 L}\ -\ \pu{0.2 L} = \pu{1.66 L}$
気相の圧力を $P\ \pu{Pa}$, 水に溶けなかった$\,\ce{N2}\,$の物質量を $n_g\ \pu{mol}$ とすると,
$$\begin{align}
PV &= nRT\\
\\
P\ \x\ 1.66 &= n_g\ \x\ \pu{8.3E3} \x\ (40 + 273) \\
\\
n_g &= \pu{6.38E-7}P\ ( \pu{mol} )
\end{align}$$
液相について水に溶けた$\,\ce{N2}\,$の物質量を $n_l\ \pu{mol}$ とすると,
ヘンリーの法則を用いて、
$$\begin{align}
n_l &= \f{ \pu{11.6 mL} }{ \pu{22.4 L/mol } } \x \f{ \pu{ P Pa} }{ \pu{1.013E5 Pa} } \x \f{\pu{0.2 L} \text{水}}{ \pu{1 L} \text{水}}\\
\\
&= \pu{1.02E-6}\ P\ ( \pu{mol} )\\
\end{align}$$
はじめに加えた$\,\ce{N2}\,$は $\f{ \pu{0.56 g} }{ \pu{28 g/mol} } = \pu{0.02 mol}$ で、
その$\,\ce{N2}\,$は気相か液相のどちらかにいます。したがって、
$$\begin{align}
n_g + n_l &= 0.02\\
\\
\pu{6.38E-7}\ P + \pu{1.02E-6}\ P &= 0.02\\
\\
\pu{1.658E-6}\ P &= 0.02\\
\\
P &= \pu{1.20E4}
\end{align}$$
液相の式の$\,P\,$に数値を代入すると、
$$\begin{align}
n_l &= \pu{1.02E-6}\ P\\
\\
&= \pu{1.02E-6}\ \x \pu{1.20E4} \\
\\
&= 0.01224
\end{align}$$
したがって、$\bold{\pu{1.2E-2 mol}}$
レベル5−2 | 体積ヘンリーが必要な読解問題
$40$℃において、$\,\ce{N2}\,$が水 $\pu{1.00 L}$ に溶ける量は $\pu{13.3 mL}$ である。
いまピストン付き容器の内部において$40$℃ で、ある量の$\,\ce{N2}\,$が水 $\pu{1.00 L}$ に接している 。このときピストンに $\pu{1.50E5 Pa}$ の圧力をかけて、平衡状態になるまで時間をおいたところ、気相の体積が$\pu{100 mL}$ となった。この状態から圧力を $\pu{1.00E5 Pa}$ にすると、気相中の$\,\ce{N2}\,$の体積は何 $\pu{mL}$ となるか。整数値で答えよ。
ただし、この系ではヘンリーの法則が成り立つとし水の蒸気圧は無視する。また、圧力が変わっても水の体積は変化しないこととする。
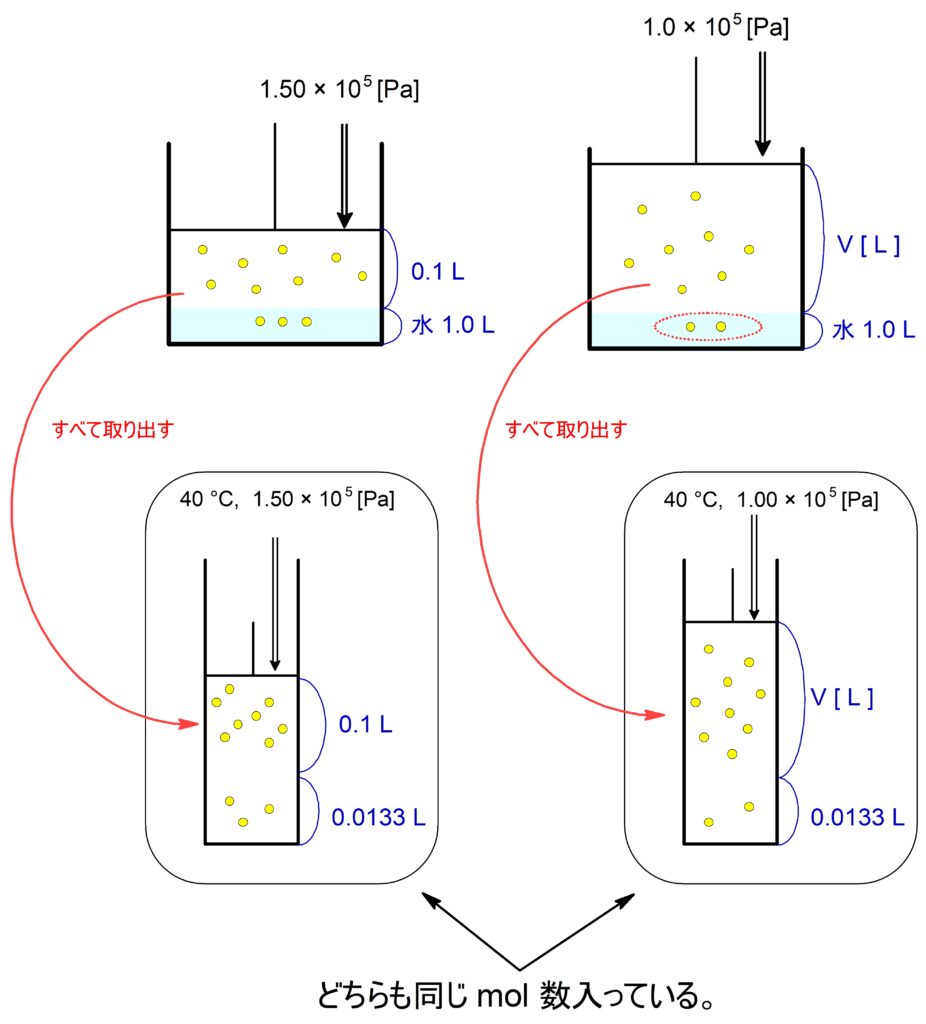

$40$℃ で$\,\ce{N2}\,$が水 $\pu{1.00 L}$ に溶ける量に関して,圧力の値が示されていません。
このときは体積ヘンリー:「そのときの圧力で測定すれば $V$ は一定」であることを用いましょう。
ヘンリーの法則の式中で圧力の値が使えないので,圧力の倍率を用いない解法を選択すれば良いのです。
この問題において水に溶けている$\,\ce{N2}\,$の体積は,そのときの圧力で測れば常に $\pu{13.3 mL}$ です!
はじめの状態において、水にとけている$\,\ce{N2}\,$も含めてすべて別のピストンに入れたとき、次の状態方程式が成り立ちます。
$$\pu{1.50E5} \x ( 0.1 + 0.0133) = nRT $$
圧力を $\pu{1.0E5 Pa}$ としたとき、求める気相の体積を $\pu{V L}$ として上記と同様に状態方程式を立てると、
$$\pu{1.00E5} \x ( V + 0.0133) = nRT $$
これら2つの式を連立すると、
$\begin{align}
\f{ \pu{1.50E5}}{\pu{1.00E5}} \x \f{ 0.10 + 0.0133 }{ V + 0.0133} &= 1 \\
\\
1.5 \x 0.113 &= V + 0.0133\\
\\
0.1695 &= V + 0.0133\\
\\
V &= 0.1562
\end{align} $
$\pu{mL}$ 単位にして整数値に直すと、答えは $\boldsymbol{\pu{156 mL}}$ です。



